EXAMPLE 4 Transform the following into Polar form
(i) x² + y² = 25 (ii) 2x + y = 0 (iii) x² + y² - 2ax = 0 (iv) x²+ y² -2by = 0 (v) x² - y² = 4 (vi) x² + y² = 4x (vii) x³ + xy² + 6x² - 2y² = 0

Solution :

1. Putting x = r cos q and y = r sin Now r² = 25    \ r ± 5 which represents a circle having centre at (0,0) and radius 5.

   

2. 2x + y = 0,    Putting x = r cos q and y = r sin q ,    we get    2(r cos q) + r sin q = 0

   

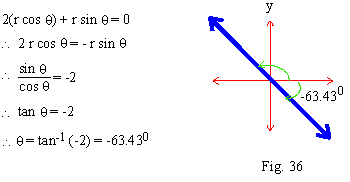
3. x² + y² - 2ax = 0, Putting x = r cos q and y = r sin q we get, r² cos² q + r² sin² q = 0

   \ r²(cos² q) = r (2a cos q)

   \ r² = r (2a cos q)

   \ r = 2a cos q which is a circle of radius "2a", passing through (0,0) and centre (2a, 0) on the polar axis.

   

4. x² + y² - 2by = 0, putting x = r cos q, y = r sin q

   \ r²(cos² q + sin² q) - 2b (r sin q) = 0

   \ r²(1) = r (2b sin q) :  \ r = 2b sin q

   which is a circle with radius '2b' and centre at (0, 2b), lies on the ^ar line through pole (0, 0) to the polar axis.

   

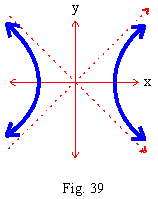
5. x² - y² = 4, putting x = r cos q, y = r sin q

   \ (r² cos² q) - (r² sin2 q) = 4

   \ r²(cos² q - sin² q) = 4

   \ r² cos²q = 4 which is a rectangular Hyperbola.

   

6. x² + y² = 4x, putting x = r cos q, y = r sin q

   \ r² (cos²q + sin² q) = 4 (r cos q)

   \ r = 4 cos q which is a circle having centre (4, 0) on the polar axis which passes through (0, 0)

7. x³ + xy² + 6x² - 2y² = 0, putting x = r cos q, y = r sin q

   x (x² + y²) + 6x² - 2y² = 0

   \ r cos q (r²) + 6 r² cos² q - 2r² sin² q = 0

   \ r cos q + 6 cos² q - 2 sin² q = 0

   \ r cos q = 2 sin² q - 6 cos² q \ r cos q = 2 - 8 cos² q

   \ r = 2 sec q - 8 cos q

   \ r = 2 (sec q - 4 cos q)

Index

7.1 Scalers & Vectors
7.2 Algebra of Vectors
7.3 Representation of a vector in a plane
7.4 Dotor Scalar product
7.5 Polar Co-ordinates
Supplementary Problems

Chapter 8