|
7.2 Algebra of Vectors
(1) Addition of two Vectors
-
Triangle Law :- The sum or resultant of two vectors
a and b is the vector formed by
placing the initial point of b on the terminal point of
a and then joining the initial point of
a to the terminal point of b .
This sum is written as r = a + b
This law is also known as Tail - Tip
rule
Parallelogram
Law :- It states that the sum or resultant of
a and b is R is the diagonal of
the parallelogram for which a and b are adjacent sides. All vectors
a, b and R are concurrent as shown
in figure 4.
Vector addition is commutative i.e.
a + b = b+ c Extension to sums of two or more vectors
is immediate.
Vector addition is associative. Observe the adjoining fig.5 we have  using tail-tip rule, for triangle  for
triangle ABC,  for
triangle OBC, c
i.e. r = ( a + b)
+ c . Also, for triangle OAC , 
i.e
r = a + (b + c).
Thus , r = ( a + b ) + c = a + (b + c).
2) Subtraction of a Vector :- It is accomplished by adding the negative of vectors i.e. a - b = a + ( - b). Note also that - ( a + b ) = - a - b .
3) Composition of Vectors :-
It is the process of determining the resultant of a system of vectors.
For this we have to draw a vector polygon, placing tail of each vector at the tip of the
preceding vector. Then draw a vector from the tail of the first vector to tip of the last vector in the system.
Later on we will show that not all vector systems reduce to a single vector. Also note that the order of
vectors are drawn is immaterial.
Free Vector :- A vector which can be shifted along its line of action or parallel to itself and whose initial point can be anywhere, is called a free vector.
Unless stated, we always refer a vector as a free vector .
Localized Vector
:- It is also known as a sliding vector. It can be shifted only along its line of action.
By the principle of transmissibility the external effects of this vector remains the same.
Bounded Vector :- It is called as a fixed vector. It must remain at the same point of action
or application.
Negative of a Vector
:- The negative of a vector u is the vector
-u which has the same direction and inclination but is of the opposite sense (of direction).
* The resultant of a
system of vectors is the least number of vectors that will replace
the given system.
Position Vector of a Point
:- If A and B are any two points then 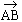 is called the position
vector of point B with reference to point A.
Usually we fix a point O and define the position vector of points with reference to O which is called the
origin of reference.
We shall use a, b, c etc. to denote position vectors of points A, B, C etc. respectively, relative to origin
O.
Unit Vector :- A vector in a given direction having unit magnitude is called a unit vector in
that direction .
It is usually denoted by  etc ( Read as n Cap). Also, note that if
U is given vector then the unit vector in the direction (or along or parallel ) to
u is given by
|
