-
The dot or scalar product of a
and b is denoted by a . b (read as a dot
b). It is defined as the product of magnitudes of the two
vectors and the cosine of the angle q
between them .
Thus a . b = a b cos q
, 0 £ q £ p
-
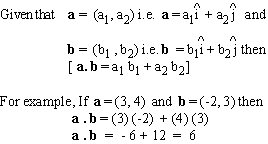
-
If a, b and c are vectors and m is a
scalar, then the following properties hold for the dot product.
1. a . b = b . a
2. a . (b + c) = a . b + a . c
3. m (a . b) = (m a) . b = a
(m b) = (a . b) m
-
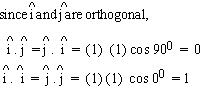
-
a .a = | a |2
-
If a and b are orthogonal (i.e.
mutually perpendicular) then a . b = 0
-
a. b = a b cos q Þ
cos q = 
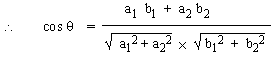
-
(a) Projection of a on the line of b
= 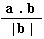
(b) Projection of b on the line of a
= 