|
CHAPTER 7 : VECTORS AND POLAR COORDINATES
7.1 Scalars and Vectors
A Scalar :- It is a quantity which can be fully expressed by its magnitude (size) e.g. mass,
length, time, temperature and any real number.
Operations with scalars follow the same rules as in elementary Algebra.
A Vector :- It is quantity having both magnitudes (size) and direction and it obeys the laws of commutation and association in addition . e.g. displacement, velocity, acceleration, force etc.
Directed Line Segment :- It is a line segment having a specific direction . Its direction is shown by an arrow head.
If the direction is from point A to B, the directed line segment is denoted by 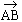 . .
Here A = initial point and B = terminal point of 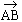
Representation of a Vector
A geometric vector is a quantity that can be represented by the directed line segment with initial point A and terminal point B ( as shown in the figure1 ) . Its magnitude is the length of the directed line segment proportional to the magnitude of the vector . The magnitude is sometimes called the norm .

Analytically a vector is represented by a symbol 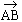 or a bold face letter
U. The magnitude of or a bold face letter
U. The magnitude of 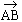 AB is written as | AB is written as | 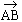 | or l (AB) or simply AB. The magnitude of
U is written as | U | or simply
U. | or l (AB) or simply AB. The magnitude of
U is written as | U | or simply
U.
Zero or Null Vector :- It is a vector of magnitude zero . It is written as
0.
It has no specific direction . Graphically it is a point .
If 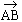 = 0 then | = 0 then | 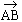 | = 0 and A and B coincides. | = 0 and A and B coincides.
Equality of Vectors :- Two vectors a and
b whose magnitudes are equal i.e. a = b and
which are in the same direction regardless of their initial points, are called equal vectors.

It can be seen that for three vectors a, b and c,
r = a + b + c = ( a + b) + c = a + (b + c) + (a + c) + b
This result can be extended to any number of vectors.
Multiplication of Vectors by Scalars
:- (A) Let m be a scalar and a be a vector then
the product ma whose magnitude in |m| times of
| a | and which is similarly or oppositely
directed to a depending upon whether m is positive or negative.
Then
for m > 0, m a is a vector of magnitude m
|a| and is in the direction of a .
for m = 0, ma is a null vector.
for m < 0, ma is the vector of magnitude - m
|a| and is exactly opposite to the
vector a
From this, it follows that (-1) a =
-a and 0 a = 0
(B) Other operations with scalars m and n are
(m + n ) a = m
a + n a
m (a + b ) = m a + m
b
mn (a) = n (ma) = (m n
a)
Linear Combination :- Let
a and b be two vectors and x and y be any real numbers. Then the vector r = xa + yb is called the linear combination of vectors a and b for example 3a + 4b , -8a + 7b . It can be extended to any finite number of vectors.
Collinear Vectors
:- Two vectors a and b are said to be collinear, if they are parallel to one
and the same line. This clearly indicates that 1) they must be coincident or (2) they must be
parallel. Also, it must be kept in mind that if two vectors are expressed as the scalar multiple of each
other then they must be collinear. i.e. if
a = xb then a and b are collinear if x ¹ 0 scalar.
Coplanar Vectors :- If vectors are parallel to a given plane, then they are coplanar. Note that if
a and b be two non-collinear vectors which can be uniquely expressed as
r = xa + yb, x , y ¹ 0 scalars, then they must be coplanar.
|