|
Here y = x2 - 2
\ y +
D y = (
x + D x )2 - 2
= x2 + 2 x
D x + (D
x)2 - 2
\ D
y = ( x2 + 2 x D
x + (D x)2 - 2) - (x2
- 2)
= 2 x D
x + (D x)2
and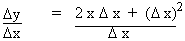 
= 2 x + (D x)
Interpretation In the figure above, PS is
parallel to x - axis and QS is parallel to y - axis. If the secant
PQ has inclination µ
with positive of x - axis, then tan µ
which is the slope of secant PQ.
Now,
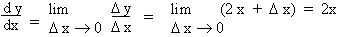
Interpretation The limiting position of
the secant PQ at P is the tangent to the curve y = x2
- 2 at P. i.e.
Q ®
P then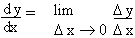 
which is the slope of tangent at P to y = x2 -
2
Example 9 If s = 3 t2 + 7 is
the distance moved by a body along a straight line from a fixed
point o in time ‘t’ (1) find Ds
in s when t varies from t = t0 to t = t0 +
D t
(2) find 
and 
and interpret the results.
(1) Here s = 3 t2 + 7,
then s + D s = 3(t
+ D
t)2 + 7
= 3 t2 + 6 t D
t + 3(D
t)2 + 7
and Ds
= 6 t D
t + 3 (D t)2
= 6 t + 3 D
t
Since Ds is the distance moved by a body in Dt ,  is the average rate of change of distance with respect to time. In other words it is the average velocity of the body in t to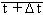 
|
