|
4.14 Derivatives of Functions In Parametric Form
THEOREM : If x = f ( t ) and
y = y ( t ) are two derivable functions
of t such that y is defined as a function of x, then
= 
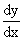Example 65 If x = at2 and y = 2 at
Find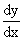
Solution : x = at2
= 2 at and y = 2 at
= 2a
= 
= 
= 
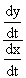
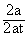
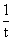
Example 66 If 
= 
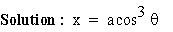
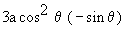
and
y =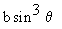 
= 
=
= 
= 
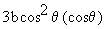
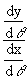
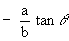
[next page]
|
