|
4.13 Logarithmic Differentiation
In order to find the derivative of
-
a function which is the product or quotient of a number of functions
or
-
a function of the form the [ f ( x ) ]g ( x ) where f ( x ) and g ( x ) are both derivable, it is usually advisable to take logarithm of the function first and then differentiate. The process is known as the logarithmic differentiation.
Example 61
If y = xx Find
y’
Solution : y = xx
Taking logarithms of both sides, we have
log y = log xx = x log x
Differentiating w. r. to x, we get
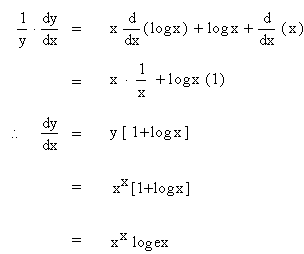
Example 62 If
y = ( log x ) log x Find 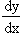
Solution: y =
( log x ) log x then we have
log y = log ( log x ) log x
= log x . log ( log x )
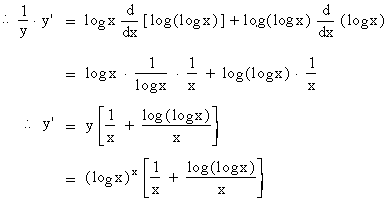
|