|
CHAPTER 5 : APPLICATIONS OF THE DERIVATIVE
5.1 Tangent and Normal Lines
The Equation of the Tangent Line to a Curve
The adjoining figure shows the graph
of the curve y = f (x), and p is a point 
on it. TPQ is the tangent to the curve at P. This is inclined at an angle
f to the positive
of x-axis.
Then as seen previously, tan f
=  represents
the slope of the tangent line TPQ to the
curve y = f (x) at the point P.
Thus, the equation of the tangent line to the curve at,
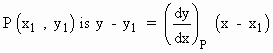
The Normal Line is defined as the line
which is perpendicular to the tangent at the point of its contact
to the curve. Therefore the slope of this normal line at point
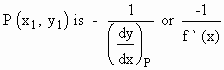
Therefore, the equation of the normal line at P to the curve y = f (x)
will be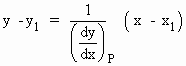 
[next page]
|
