Perimeters of similar triangles: Perimeters of similar triangles are in the same ratio as their corresponding sides and this ratio is called the scale factor.

In figure 5.6 there are two similar triangles . D LMN and D PQR.

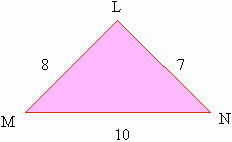
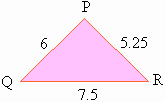
Figure 5.6

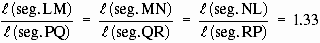
This ratio is called the scale factor.

Perimeter of D LMN = 8 + 7 + 10 = 25

Perimeter of D PQR = 6 + 5.25 + 7.5 = 18.75

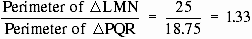
Thus, the perimeters of two similar triangles are in the ratio of their scale factor.

Areas of similar triangles: The ratio of the areas of two similar triangles is equal to the ratio of the squares of the corresponding sides, i.e. the square of the scale factor.

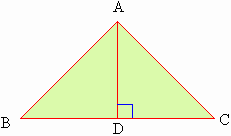
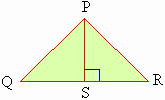
Figure 5.7

D ABC ~ D PQR

To prove that

Draw perpendicular from A and P to meet seg.BC and seg.QR at D and S respectively.

Since D ABC ~ D PQR

also Ð B @ Ð Q

In D ABD and D PQS

also Ð B @ Ð Q and Ð ADB @ Ð PSQ

\ D ABD ~ D PQS by A A test.

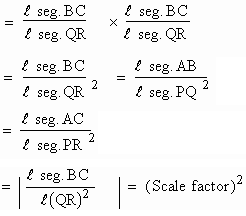
Thus the areas of two similar triangles are in the same ratio as the square of their scale factors.

[next page]

Index

5.1 Introduction
5.2 Ratio And Proportionality
5.3 Similar Polygons
5.4 Basic Proportionality Theorem
5.5 Angle Bisector Theorem
5.6 Similar Triangles
5.7 Properties Of Similar Triangles

Chapter 6