5.4 Basic Proportionality Theorem
If a line is drawn parallel to one side of a triangle and it intersects the other two sides at two distinct points then it divides the two sides in the same ratio.
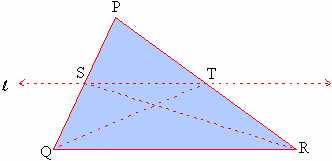
Figure 5.4
Figure 5.4 shows triangle PQR with line l
paralled to seg.QR. l
intersects seg.PQ and seg.PR at S and T respectively.
To prove that 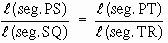
Join S to R and Q to T
Consider D
PTS and D QTS

Areas of triangles with same height are in the ratio of their bases.
Similarly 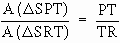
But A ( DQTS
) = A ( D SRT ) as they have a
common base seg.ST and their heights are same as they are between
parallel lines.
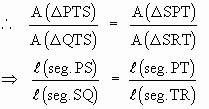
Thus the line l
which is parallel to seg.QR divides seg.PQ and seg.PR in the same
ratio.
[next page]
|