5.5 Angle bisector theorem
In a triangle the angle bisector divides the opposite
side in the ratio of the remaining sides. This means that for a
D ABC ( figure 5.5) the bisector of
Ð A divides BC in the ratio
 . .
Figure 5.5
To prove that 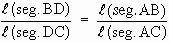
Through C draw a line parallel to seg.AD and extend seg.BA to meet it at E.
seg.CE çç
seg.DA
Ð
BAD @ Ð
AEC , corresponding angles
Ð
DAC @ Ð
ACE , alternate angles
But Ð
BAD = Ð DAC , given
\
Ð AEC
@ Ð
ACE
Hence D AEC is an
isosceles triangle.
\
seg.AC @ seg.AE
In D
BCE AD çç CE

Thus the bisector divides the opposite side in the ratio of the remaining two sides.
[next page]
|