|
\ 
= 8
(1) [(1)2 - 2]3
= 8 [-1] = - 8
which is the slope of tangent to this curve at point (1, 1).
Now equation of the tangent to this curve at (1, 1) will be
y - y1 = m (x - x1)
Now m = - 8 and (x1, y1) = (1, 1)
\ y - 1 = - 8 (x - 1) i.e.
y - 1 = - 8x + 8
\ 8x +
y - 9 = 0
® Equation of the tangent
line.
Example 30
At what point on y =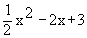 
is the tangent perpendicular to that at the point (1, 0) ?
Solution : y =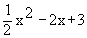
Differentiating w.r.to x we get,
=
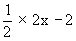
= x - 2
\ 
= 1 - 2 = -1
\ The slope (m1)
of the tangent to the curve at (1, 0) is -1.
If m2 is the slope of a perpendicular line to
this tangent at (1, 0)
Then we have m1 x
m2 = - 1 Þ m2
= +1
\ 
= x1 - 2 = 1 \
x1 = 3
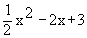
Putting in y =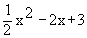
we get, y = 
= 3/2
\ The required point is (3 , 3/2)
|
