|
Example 15
Evaluate 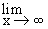
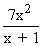
Solution : L = 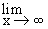
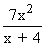
= 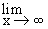

= 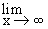

= 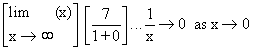
=  [7]
[7]
= + •
Example 16 Evaluate 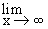 ( x5 - x3 - 7x )
( x5 - x3 - 7x )
Solution : Let L = 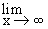 ( x5 - x3 - 7x )
( x5 - x3 - 7x )
= 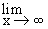
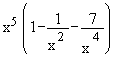
= 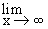  .
. 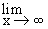
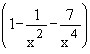
= 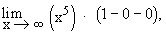

= 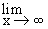 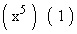
L = •
Note:
Limits at infinity describe the behavior of functions when its independent variable increases or decreases without bound. In either cases if L is the limit
then 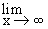 f (x) = L or f (x) = L or 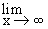 f (x) = L. (L = real number) f (x) = L. (L = real number)
Also, f(x) said to have horizontal asymptote at f(x) = L.
So, in Example 12, f(x) has a horizontal asymptote at y = 1/4.
in Example 13, f(x) has a horizontal asymptote at y = 8.
in Example 14, it is y = c/2, c is a real number.
in Example 15, f(x) has no asymptote as x increases without bound.
in Example 16, f(x) has no asymptote as x decreases without bound.
|