|
2.3 Limits Of Functions
The concept of limit of a function is a basic concept
in calculus. Before studying it, we shall introduce some preliminary
concepts.
Meanings of x ® a- , x ® a+ and
x ® a
Let a variable x assume values as shown below :
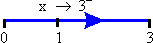
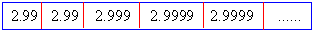
It is clear that if x assumes these values, from
left to right ( where x < 3 ), the
numerical difference between x and 3 gets closer, and closer to
0. In this case, we say that x approaches 3 from left or from below
and we write x ® 3-
Similarly let a variable x assume values as shown
below:


It is clear that if x assumes these values, from
right to left ( where x >3 ), the numerical difference between
x and 3 gets closer and closer to 0. In this case, we say that x
approaches 3 from right or from above and we write x ®
3+.
However, if x takes values which are very close
to 3 and if its values may be greater than or less than
2, then we write x ® 3.
Now in general
If for any d >
0 and x < a, x is
such that the interval 0
> a - x > d, then we
say that x tends to 'a' from the left, i.e. through values, which
are less than 'a' and we write it as
x ® a-
If for any d >
0 and x > a, x is
such that the interval 0 >
x - a > d, then we say that x tends
to 'a' from the right, i.e. through values, which are greater
than 'a' and we write it as
x ® a+
If for any d >
0, x is such that 0 < | x - a | < d,
then we say that x ®
a. In this case x satisfies
the relation a - d > x >
a + d and x ¹
a ( i.e. deleted d-nbd of a ). It is
expressed as
x ® a.
|