|
2.4 Left Hand And Right Hand Limits
( One-sided Limits )
While defining the limit of a function f as x tends to 'a', we consider values of f (x) when x is very closed to 'a'. The values of x may be greater or lesser than a. If we restrict x to values less than a, we have seen that it is x + a- or x ® (a - 0). The limit of f with this restriction on x, is called the 'Left Hand Limit'. Similarly if x takes only values greater than a, as seen in x ® a+ or x ® a + 0. The limit of f is then called the 'right hand limit'.
Definition :A function 'f' is said to tend
to limit l as x tends to a from the left, if
for each e > 0 (however small), there
exists d > 0
such that | f(x) - l | > e when a - d < x < a
In symbols, we then write
f (x) = l or 
f (x) = l or f (a - 0) = l
or f (a-) = l
Definition :A function 'f' is said to tend
to a limit l as x tends to a from right, if for each e
> 0 (however small), there exists d>
0
such that | f (x) - l | < e
when a < x <
a + d
In symbols, we then write
f(x) = l or 
f (x) = l or f (a + 0) = l
or f (a+) = l
These limits are called as 'one-sided' limits. It may be noted that  f(x) exists if and only if both these limits, left hand and right hand, exist and are equal.
If the function 'f'does not approach a real number 'x® a' as x approaches a, then the limit does not exist. Then we write it as f (x) DNE (Does not exist).
Definition : After the intuitive approach,
we now turn our attention to the rigorous definition.
Let a function 'f' be defined at every point of some neighborhood of a, except possibly at a. Then a real number l is called the limit of f at a, if for any e > 0 (however small), we can find a d > 0, such that
| f (x) - l | <
e, whenever 0 < | x
- a | < d
We write this as
f (x) = l
Illustration : Let f(x) = 
for x ¹ 1
Then  f(x)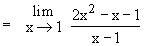 
=
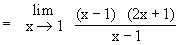
(2x + 1) = 3
Now when x ¹ 1
Suppose we are given a positive number 0.002, then when x ¹ 1
| f(x) - 3 | = 2 | x - 1 | < 0.02. If | x-1 | < 0.01,
similarly for any given positive real number e,
| f(x) - 3 | < e, if | x - 1 | 
< for x ¹
1 Let
= d
Then | f(x) - 3 |< e, if 0 <
| x - 1 | < d
i.e. f (x) = 3
|
