|
Example 1 Find the right hand and the left hand limits of a function 'f ' as follows:
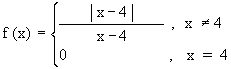
Solution : When x > 4 | x - 4 | = x - 4
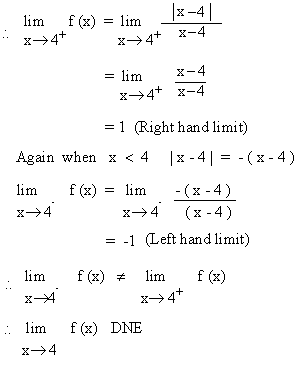
Example 2 Show that  4x = 8
Solution : For | 4x - 8 | <
e if | 4 (x-2) | < e
i.e. if 4 | x - 2 | < e i.e., if | x - 2 | < e/4
Thus d = e/4 ; we
find, therefore, that every e>
0, a number d > 0 where d
= e/4, satisfying
| 4x - 8 | < e for
all | x - 2 | < d
Hence 4x = 8
Example 3 If f (x) =  ,
x ¹ 0 
f (x) DNE. Prove this statement.
Solution : If x > 0, we
have f (x) = 
= 1
\ 
f (x ) = 1
Example 4 Show that
sin 
, x ¹ 0 is oscillating between -1 and
+1.
Solution : Let sin , x ¹ 0
We observe that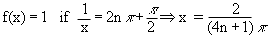 
and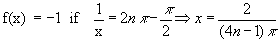 
Thus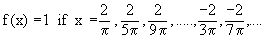 
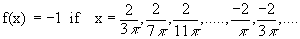
Further we know that -1 £ sin  £ 1
\ The graph of y = sin lies between y = -1 and y = +1 and oscillates up and down very rapidly as x®0. This behavior of the function is expressed by saying that the limit of f(x) as x®0 DNE and it is further described by saying that f(x) is oscillatory, the limits of oscillation being -1 and +1.
|
