|
2.7 Limits Of Trigonometric Functions
The trigonometric functions have following important limit properties:
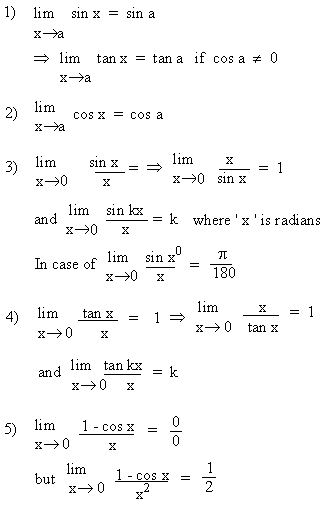
Example 1
Evaluate 
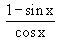
Solution : Let L =
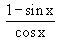
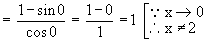
Example 2 Evaluate 
( 1 + cot x )
Solution : Let L =
( 1 + cot x )
= 1 + cot ( p/4
) = 1 + 1 = 2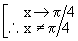 
Example 3 Evaluate 
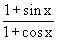
Solution : Let L =
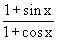
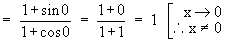
Example 4 Evaluate 
cot x
Solution : Let L =
cot x =
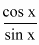
Here sin x ® 1 and cos x ®
0 as x ® 0 and x > 0 ( in the
1st quadrant). Therefore the function cot x increases without bound
and 
cot x = + ¥.
It has a vertical asymptote at x = 0.
Example 5 Evaluate
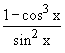
Solution : Let
L =
|
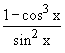
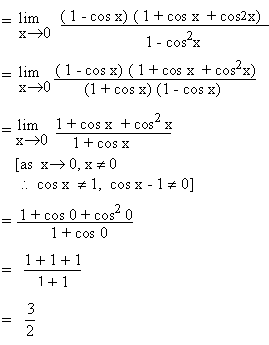
