|
EXAMPLE 11
Sketch the graph of y = 10 sin x + 2 sin (3x +
p/2). Find the period, maxima and minima.
Solution:
The function y = 10 sin x + 2 sin (3x + p/2) has
(i) Period = 2p
(ii) Maximum = 10.5 at maxima = 1020
(iii) Minimum = -10.5 at minima = 2820

Fig. 33
EXAMPLE 12
Find the period, phase shift and the location of the asymptotes for the function 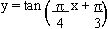
Solution :
i) The period of the function
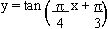 is obtained by is obtained by

ii) The phase shift of the function is given
by  since the phase shift is positive, it is to the left. since the phase shift is positive, it is to the left.
iii) Now the asymptotes can be found by solving (bx + c)
=  and (bx + c) = - and (bx + c) = - as as

Note I
i) The general equations of tangent and cotangent functions are-
y = d + a tan (bx + c) and y = d + a cot (bx + c)
ii) \ Period = p / b
iii) The phase shift = |c / b| when c/b < 0 then the shift is to the right and when c / b > 0 then
the shift is to the left.
iv) Asymptotes are obtained on solving bx + c =
p /2 and bx + c = -p /2.
v) Since tangent and cotangent are unbounded the variable 'a' does not represent
"amplitude".
vi) The vertical shift is represented by "d" .
Note II For Secant and Cosecant functions
i) Amplitudes are not defined.
ii) As sec and csc are reciprocals of sin and cos, they have the same period
(2p/b) and
phase shift = | c / b |.
iii) Asymptotes of these functions are obtained by solving the two equations bx + c = 0 and
bx + c = 2p.
|