|
EXAMPLE 13
Find the period, phase shift and the location of the asymptotes for the function
y = 1/3 sec (p/2 + p/4).
Solution
i) The period of the function is 
ii) The phase shift is |c/b| =  = 1/2 > 0
\ phase shift is to the left.
iii) The asymptotes are obtained as,
bx + c = 0 .....(i) bx + c = 2p
.....(ii)
EXAMPLE 14
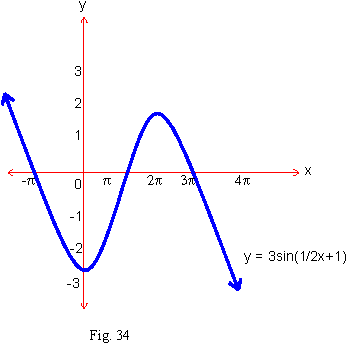
State the amplitude, period and phase shift (if non zero). Also draw graphs of
y = -3 sin (1/2x + 1) and y = -3 sin (1/2x + 1) + 4
Solution : y = -3 sin (1/2x + 1)
Note : On comparing with y = a sin (bx + c) we get a = -3, b = 1/2 and c = 1 and
-3 sin (1/2x + 1) = -3 sin 1/2 (x + 2). Thus the amplitude is |a| = 3, period =
 = 4p
and phase shift is |c/b| =  = 2
Graphs of y = -3 sin (1/2x + 1) and y = -3 sin (1/2x + 1) + 4 on translating the graph 4
units upward we get the graph of y = -3 sin (1/2 x + 1) + 4
|
