|
Example 10
Show that
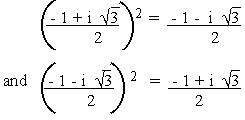
Solution
 
Note that 
with 1 are nothing but the cube roots of unity (i.e. 1).
They are denoted by w, w2,
1 and they are related by a relation 1 + w
+ w2 = 0
Example 11
(a) Find the value of x3 + 2x2 - 3x + 5 if
x =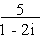 
Solution
\ x = 1 + 2i x - 1 = 2i
. squaring both sides we get
(x - 1)2 = (2i)2 i.e. x2- 2x
+ 1 = 4i2 \ x2
- 2x + 1 = - 4 \ x2 - 2x +
5 = 0
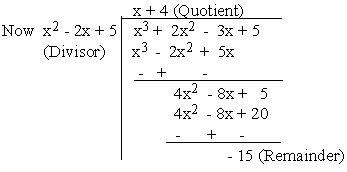
By division algorithm, Dividend = (Divisor) (Quotient) + Remainder
\ x3 + 2x2 -
3x + 5 = ( x2 -
2x + 5) (x + 4) - 15
= (0) (x + 4) - 15
= -15
(b) Find the value of x4 - 4x3 + 6x2
- 3x + 66 if x = 3 + 2i
Solution
x = 3 + 2i x - 3 = 2i
Squaring both the sides , x2 - 6x + 9 = -4 i.e.
x2 - 6x + 13 = 0
x2 + 2x + 5
\ x4 - 4x3 + 6x2
- 3x + 66 = (x2 - 6x + 9) ( x2
+ 2x + 5) + (x + 1)
= (0) (x2 + 2x + 5) + ( 3+ 2i + 1)
= 4 + 2i
Example 12
Find the modulus and argument of (-1 + i)
Solution
Let a + bi = -1 + i Þ a = -1
and b = 1
then modulus of (-1 + i) = 
2 units
and the amplitude q = tan-1(b
/a) = tan-1 (1 / -1) = 1350 or 
Example 13
Find the modulus and amplitude of (1 - cos a)
+ j sin a
Solution
Let a + bi = (1 - cos a) + j sin a
and express in the polar form.
\ a = (1 - cos a)
= 2 sin2 (a / 2) and b = sina
= 2 sin (a / 2) cos (a
/2)
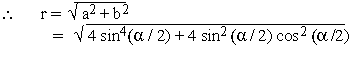
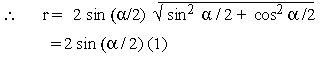
\ Modulus is
2 sin (a / 2)
Also,
cos q = 
= sin (a / 2)
and
sin q =
= cos (a/2)
\ case (1) If sin a
/ 2 ³ 0 then
z = a + bi = 2 sin a/ 2 (sin a
/ 2 + j cos a/2 )
.... using z = r (cos q + j sin q)
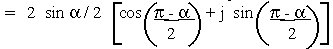
case (ii) If sin a / 2 < 0 then
z = 2 sin (a/2) - sin (a
/ 2) - j cos (a / 2 ) = - 2 sin (a/2)
[next page]
|
