|
CHAPTER 9 : APPLICATIONS
9.1 The Expression A sin
wt + B cos wt
The equation y = A sin wt + B cos
wt .........(1)
Put A = a cos a and B = a sin
a in equation (1) we get
y = ( a cos a ) sin
wt + (a sin a) cos wt
y = a [ sin wt cos a +
cos wt sin a]
y = a sin (wt + a)
........(2)
The two equations (1) and (2) are equivalent expressions.
and Asin wt + Bcos wt = a sin
(wt + a) given that 'a' is an angle with a point P (A, B) on its terminal side.
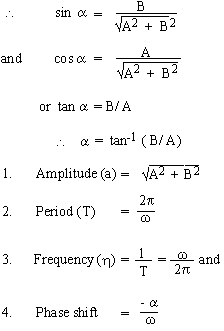
Example 1 Transform y = 3 sin 2t + 4 cos 2t to the form y = a sin
(wt + a). Also find period, amplitude, frequency and phase shift.
Solution
y = 3 sin 2t + 4 cos 2t. Comparing with y = A sin wt + B cos wt, we get A = 3, B = 4 and w = 2.
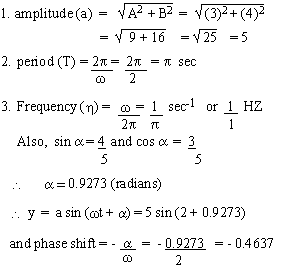
Example 2 Convert y = sin
p t + cos p t to the form y = a sin (wt + a). Also find its period, frequency, amplitude and phase shift.
Solution
|
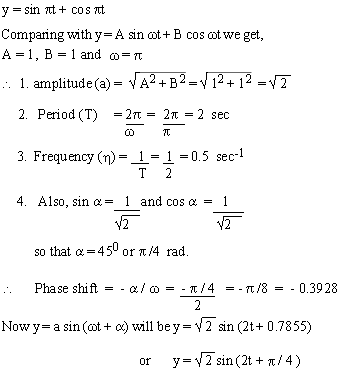
