|
Example 14
Express in the polar form (a) 1 + j
Solution
Let z = a + bj = 1 + j
so that a = 1 and b = 1
\ r =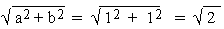 
and cos q = 
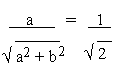= cos 450
with sin q =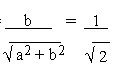
= sin 450 since reference angle q
= 450
\ The required polar form thus, z =
r (cos q + j sin q)
will be
z =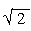 
(cos 450 + j sin 450 )
i.e.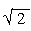
cos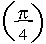 
+ j sin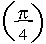
(Fig2)
(b)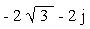 
Solution
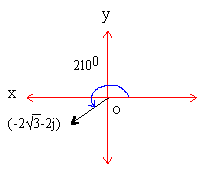
Let z = a + bj = 
- 2j so that
a =
and b = -2
\ r =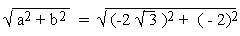 
\ r = 
= 4 also, cos = 
and sin q =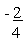 
= -1/2 \ The reference angle
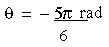or - 1500 or 2100
\ The required polar
form of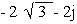 
is
4 (cos 2100+ j sin 2100)
Example 15
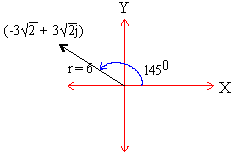
Express in the a + bj form (a) 6 (cos 1350 + j sin
1350)
Solution
Let z = r (cos q + j sin q)
= 6 (cos 1350 + j sin 1350)
\ z = 6 [ cos (900 + 450
) + j sin ( 900 + 450 ) ]
\ z = 6 [ - sin 450 + j cos
450 ]
\ z = 6
(Fig3)
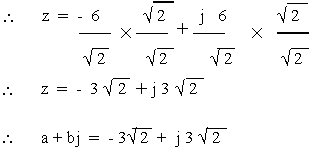
The Polar form of a Complex number
Every complex number z = x + iy or z = a + bi can always be put
in the form
r (cos q + i sin q)
i.e. x + iy = r (cos q + i sin q)
\ x = r cos q
and y = r sin q
x2 + y2 = r2 i.e. r2
= 
and tan q =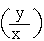 
or q = tan-1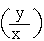
r and q are both real and non-negative.
Thus x + i y = r (cos q + i sin q)
= r eiq is known as the Polar form of a complex number.
Remarks
1) 1 = cos 0 + i sin 0
\ r = 1 and q
= 0
2) -1 = cos p
+ i sin p
\ r = 1 and q
= p i.e. 1800
3) i = cos(p
/ 2) + i sin (p / 2) \ r
= 1 and q = p
/ 2 i.e. 900
4) -i = cos (p
/ 2) - i sin (p / 2) \
r = 1 and q = - p
/ 2 i.e. - 900
About Argument (or Amplitude)
We know that the angle q is called the
amplitude (or argument) of the complex number z and denoted by amp
(z) or arg (z). Thus q = amp (z) or arg
(z) = tan-1( y / x)
Remarks
1) The value of q which lies between
- p and p
is called the principal value.
2) If a is the principal value of the amplitude, (2n p
+ a) where n is any integer is called
the general value of the amplitude.
3) arg (z1 z2) = arg z1 + arg z2
4) arg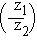 
= arg z1 - arg z2
[next page]
|
