|
4.2 The Addition Formulas (Identities)
In this part, we will study the trigonometric ratios
(functions) of sum and difference of two angles.
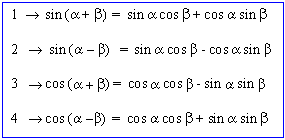
Verification
1) For all real values of a
and b cos (a
- b) = cos a
cos b + sin a
sin b.
Consider a unit circle as shown in the figure.
Let R, P, Q, be three points on it such that Ð
ROP = a, Ð
ROQ = b so that
ÐQOP = a - b.
Set the centre of the circle at the origin of the rectangular Cartesian
system. Let x- axis be along OR. Draw Y- axis.
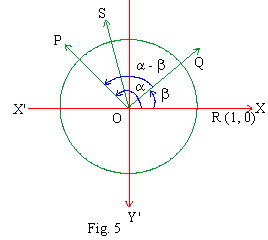
Here we have OR = OP = OQ = 1
\ R º
(1,0), P º ( cos a
, sin a ) and Q º
(cos b, sin b)
..... (Using x = r cos q, y = r sin q
i.e. changing to polar coordinates)
\ By distance formula,
PQ2 = (cos a
- cos b)2 + (sin a
- sin b)2
= (cos2 a + sin 2
a ) + (cos2 b
+ sin2 b) - 2 (cos a
cos b + sin a
sin b)
= 1 + 1 - 2(cos a cos
b + sin a
sin b )
\ PQ2= 2
-2 (cos a cos b
+ sin a sin b)
.......(1)
Take point S on the circle so that ÐROS
= a-b
\ S º
[cos (a - b),
sin (a - b)]
Then by distance formula,
RS2 = [cos (a- b)
-1 ]2 + [sin (a -b
)]2
= cos2 (a - b)
+ sin2(a - b)
-2 cos (a - b)
RS2 = 2 - 2 cos (a - b
)
........(2)
Since ÐQOP = ÐROS,
their corresponding arcs PQ and RS are also equal which implies
that the corresponding chords PQ and RS are also equal.
\ from (1) and (2) we
get
2 - 2 cos (a - b)
= 2 - 2 (cos a cos b
+ sin a sin b
)

put a = x and b
= -y in
cos (x - y ) = cos x cos y + sin x sin y, x, y Î
R
We get cos (a + b)
= cos a cos (-b)
+ sin a sin ( -b)
but cos (-b) = cos b
and sin (-b) = - sin b

Reduction to Functions of Positive Acute
Angles And Negative Acute Angles.
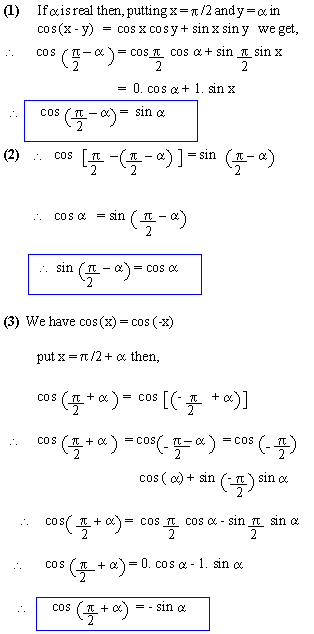
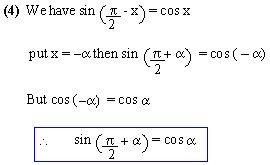
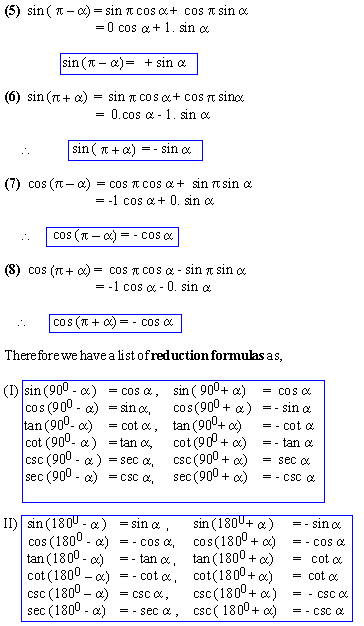
Note that * 1) sin (n
900 ± a)
= ± cos a,
n Î N and n is odd
* 2) cos (n 900 ± a)
= ± sin a,
n Î N and n is odd
* 3) sin (n 900 ± a)
= ± sin a,
n Î N and n is even
* 4) cos (n 900 ± a)
= ± cos a,
n Î N and n is even
The sign on R.H.S is determined by the Quad. of
the angle in L.H.S using ` A S T C'
Example 1 Evaluate sin 800cos
1300+ cos 800 sin 1300
Solution Let a = 800and
b = 1300 then sin 800
cos 1300 + cos 800sin 1300 = sin
a cos b +
cos a sin b
= sin (a + b)
= sin (800+1300)
= sin (2100)
= sin (1800 + 300)
= - sin 300
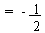
Example 2 Find the value of
i) cos 4800 ii) tan (- 9450) iii) sin 46200
Solution
- cos 4800= cos ( 5
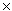 90 0 + 300) = - sin 300 = -1/2
90 0 + 300) = - sin 300 = -1/2
As angle in Quad II, cosine ratio is negative.
.... [Note : 4800 = 3600 + 1200
coterminal to 1200. Hence in Quad. II ]
- tan ( -9450) = - tan (9450)
.... \ tan (- q)
= - tan q
= - tan (10  90
0 + 450) 90
0 + 450)
= - tan 450 .... \
tan (n900+ a ) = + tan a
for n is even and angle is in Quadrant III.
= -1
[Note : 945 = 2 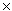 360 + 225 coterminal to 225. Hence in Quad. III]
360 + 225 coterminal to 225. Hence in Quad. III]
Example 3
Express of the following in terms of a function
of  : :
(i) sin (5400+  ) (ii) csc (-9000+
) (ii) csc (-9000+  )
(iii) tan ( )
(iii) tan ( - 3600)
(iv) cos (- 4500- - 3600)
(iv) cos (- 4500-  ) )
Solution
- sin (5400+
 )
= sin ( 6 )
= sin ( 6 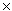 90O
0+ 90O
0+  ) = - sin ) = - sin
 .....[n is even and
angle is in Quad III] .....[n is even and
angle is in Quad III]
- csc (- 9000+
 )
= csc (10 )
= csc (10 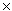 900
+ 900
+  ) = - csc ) = - csc  [csc (-x) = -csc x, n is even and angle is in Quad. II]
[csc (-x) = -csc x, n is even and angle is in Quad. II]
- tan (- 3600 ) = tan (- 4
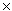 900 +
900 +  ) = - (-tan
) = - (-tan  ) [tan
(-x) = -tan x, n is even and angle is in Quad.IV] ) [tan
(-x) = -tan x, n is even and angle is in Quad.IV]
- cos (- 4500 -
 ) = cos ( - 5
) = cos ( - 5 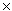 900- 900-
 ) = - sin ) = - sin  [cos (-
[cos (-  ) = cos ) = cos  ,
n is odd and angle is in Quad (I)] ,
n is odd and angle is in Quad (I)]
Example 4
Evaluate tan (-9450) and sin (46200)
Solution
- tan (-9450) = - tan 9450 .....[tan (-
 ) = - tan ) = - tan  ] ]
= - tan (10 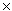 90
0+ 450 ) 90
0+ 450 )
= - tan 450 .....[n is even and
angle is in Quad III ]
= -1
- sin 4620 0 = sin ( 51
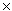 900+ 300)
900+ 300)
= -cos 300 .....( n is even and
Quadrant IV)
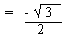
Example 5 Prove that tan 4950cot
(- 4050) + cot ( 4950) tan (- 5850
) = 2
Solution
L.H.S = tan 4950 cot (- 4050)
+ cot ( 4950) tan ( -5850)
= tan 4950 (- cot 4050)
+ cot 4950(- tan 5850)
.....[cot (-  ) = -
cot ) = -
cot  and tan (- and tan (-  ) = -tan
) = -tan  ] ]
= - tan (5 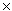 900+ 450) cot (4
900+ 450) cot (4 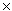 900 + 450) - cot ( 5
900 + 450) - cot ( 5 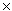 900+ 450)
900+ 450) 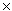 tan ( 6
tan ( 6  900
+ 450) = - (- cot 450) (cot 450)
- (- tan 450) (tan 450) 900
+ 450) = - (- cot 450) (cot 450)
- (- tan 450) (tan 450)
= 1  1 + 1
1 + 1  1
.....[cot 450 = tan 450= 1] 1
.....[cot 450 = tan 450= 1]
= 2
[next page]
|