|
4.3 The multiple - angle (Double &
Half Angle) Formulas
With the help of the sum and difference (compound
angle formulas studied in the previous article, we will express
the trigonometric functions of angle 
in terms of /2 ).
For any angle
(1) \ sin 2
= 2 sin cos
then
\ sin
= 2 sin ( /2) cos (/2)
(2) \ cos 2
= cos2 -
sin2
\ cos
= cos2(
/2) - sin2(
/2)
\ cos 2
= 2 cos2
-1
\ cos
= 2 cos2(
/2) - 1 and
\ cos 2
= 1 - 2 sin2
\ cos
= 1 - 2 sin2 (/2)
From the above formulas, we derive the following
formulas
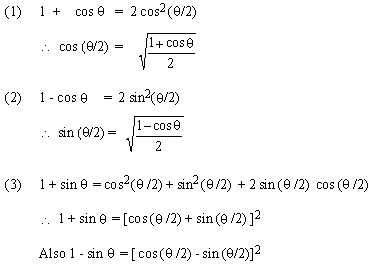
EXAMPLE 1 Find the value of
cos 150, using the ratios of 300only.
Solution:
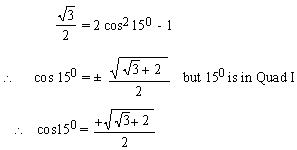
EXAMPLE 2 Find the exact value
for sin 1050using the half- angle identity.
Solution :
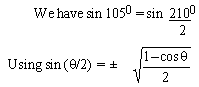
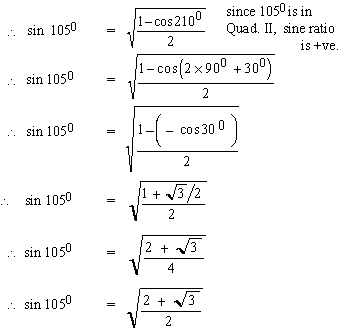
EXAMPLE 3 Find the exact value
of sin (292.50 ) using the half angle formulas.
Solution : /2
= 292.50 is in Quad. IV in which sine ratio is negative.
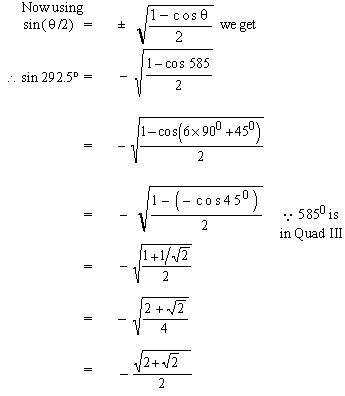
EXAMPLE 4
Find the values of sine and cosine of 
. Given that sin =
5 / 13 , is in Quad
II
Solution:
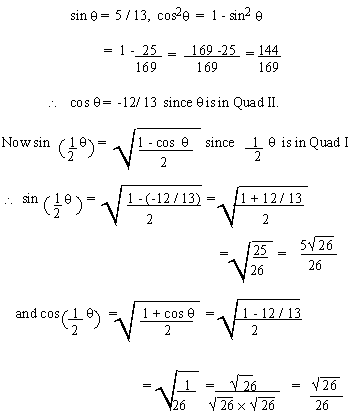
EXAMPLE 5 Find the exact value
for cos 1650 using half- angle identity.
Solution:
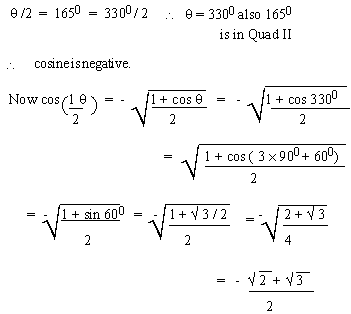
EXAMPLE 6 Find sin 22.50,
cos 22.50 and tan 22. 5 0using the half angle
formulas.
Solution:
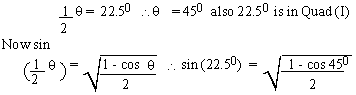
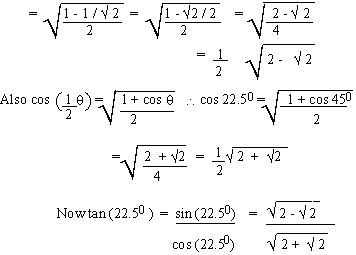
EXAMPLE 7 
in terms of sin x and cos x
Solution:
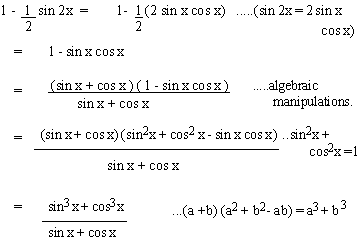
EXAMPLE 8 Prove that 
Solution
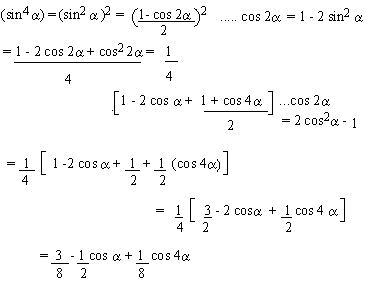
EXAMPLE 9
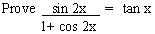
Solution:
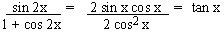
EXAMPLE 10
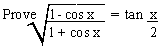
Solution:
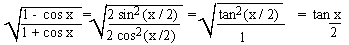
EXAMPLE 11
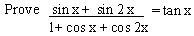
Solution:
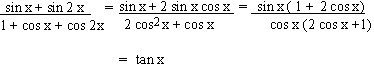
EXAMPLE 12
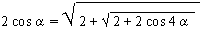
Solution:
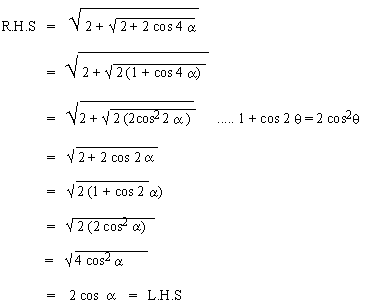
[next page]
|
