Example In a partially destroyed laboratory record of an analysis of correlation data, the following results are legible:

What are (1) Means of x’s and y’s (2) the coefficient of correlation between x and y (3) the standard deviation of y ?

Solution:

1. Means:

   8 x - 10 y = -66 ----- (1)

   40 x - 18 y = 214 ----- (2)

   Solving (1) and (2) as

   40 x - 50 y = -330 ----- (1)

   40 x - 18 y = 214 ----- (2)

   -32 y = -544

   y = 17

   \ Mean of y’s 17

   Substituting y = 17 in (1) we get 8x - 10 ´ 17 = -66

   or 8x = 104 \ x = 13

   \ Mean of x’s = 13

2. Coefficient of correlation between x and y

   40 x = 18 y + 214

       

   

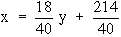
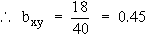
   Also -10 y = - 8 x - 66

   

   [next page]

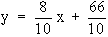
Index

6. 1 Introduction
6. 2 Correlation
6. 3 Types of Correlation
6. 4 Degrees of Correlation
6. 5 Methods of determining correlation
6. 6 Coefficients of Correlation for Bivariate Grouped Data
6. 7 Probable Error
6. 8 Rank Correlation Coefficient
6. 9 Linear Regression