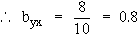
Therefore,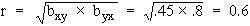

3. Standard deviation of y

   \ Variance of x i.e. s x² = 9 \ s x = 3

   Now byx =

   \ s y = 0.4

Example From 10 observations of price x and supply y of a commodity the results obtained S x = 130, S y = 220, S x² = 2288, S xy = 3467

Compute the regression of y on x and interpret the result. Estimate the supply when the price of 16 units.

Solution: The equation of the line of regression of y on x

y = a + b x

Also from normal equations

S y = n a + b S x and S xy = a S x + b S x²
we get

220 = 10 a + 130 b Þ (1)

3467 = 130 a + 2288 Þ (2)

Solving (1) and (2) as

2860 = 130 a + 1690 b
3467 = 130 a + 2288 b

On subtraction
\ 607 = 598 b \ b = 1.002

Putting b = 1.002 in 220 = 10 a + 130 b, we get a = 8.974.

Hence the 3 equation of the line of regression of y on x is
y = 8.974 + 1.002 x

Index

6. 1 Introduction
6. 2 Correlation
6. 3 Types of Correlation
6. 4 Degrees of Correlation
6. 5 Methods of determining correlation
6. 6 Coefficients of Correlation for Bivariate Grouped Data
6. 7 Probable Error
6. 8 Rank Correlation Coefficient
6. 9 Linear Regression