6.6 Coefficient Of Correlation For Bivariate Grouped Data
When the number of observations is very large, we need to arrange the data into different classes, which are either discrete or continuous. Items having values falling in a particular class are placed together and those having values falling in another class are placed together. Due to this the whole data is divided into horizontal rows and vertical columns, with one variable placed horizontally and the other placed vertically. The table so obtained is a two-way frequency distribution table and is called the correlation table or Bi-variate frequency distribution table. The formula for calculating and for bi-variate distribution is given by
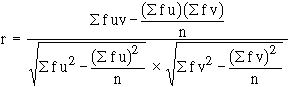
STEPS:
-
First write down the mid-points of x along a horizontal raw and those of y along a vertical column.
-
Find 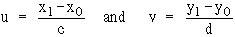
-
Multiply each frequency by the corresponding value of u then by corresponding value of v to get fuv. Write these numbers in the same box at the top.
-
Add the frequencies horizontally, and write down the total. Similarly add the frequencies vertically and write down its total.
-
Multiply this additions of x by u to get f u.
-
Multiply this addition of y by v to get f v.
-
Multiply these frequencies by the square of u to get f u2.
-
Multiply these frequencies by the square of v to get f v2.
-
Add horizontally ( or vertically ) the top numbers denoting f u v written in each box ( or cell )
Write down S f u, S f u2, S f v, S f v2 and S f u v and then use the above formula.
Example Calculate the coefficient of correlation
for the following data.
|
Age (years) of Husband
|
Age (years) of wife
|
Total
|
|
10 -20
|
20 -30
|
30 -40
|
40 -50
|
50 -60
|
|
10 - 25
25 - 35
35 - 45
45 - 55
55 - 65
|
5
3
|
3
15
11
|
11
14
7
|
7
12
3
|
3
6
|
8
29
32
22
9
|
|
Total
|
8
|
29
|
32
|
22
|
9
|
100
|
|
Index
6. 1 Introduction
6.
2 Correlation
6. 3 Types of Correlation
6. 4 Degrees of Correlation
6. 5 Methods of determining correlation
6. 6 Coefficients of Correlation for Bivariate Grouped Data
6. 7 Probable
Error
6. 8 Rank Correlation Coefficient
6. 9 Linear Regression
Chapter 7
|