Example The two regression equations of the variables x an y are

Solution:

1. Calculation of Mean

   

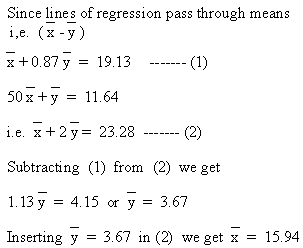
   \ Mean of x’s = 15.94 and Mean of y’s = 3.67

2. Calculation of ‘ r ’

   x = 19.93 - 0.87 y

   Therefore,

   and y = 11.64 - 0.50 x

   Therefore,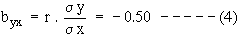

   From (3) and (4)

   

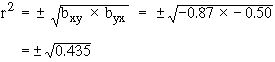
     r = ± 0.66

   But regression coefficient are negative

   r = - 0.66

   [next page]

Index

6. 1 Introduction
6. 2 Correlation
6. 3 Types of Correlation
6. 4 Degrees of Correlation
6. 5 Methods of determining correlation
6. 6 Coefficients of Correlation for Bivariate Grouped Data
6. 7 Probable Error
6. 8 Rank Correlation Coefficient
6. 9 Linear Regression