|
Example 30
A right circular cylinder has to be made, so that
the sum of its radius and its height is 6 m. If its volume is maximum,
find its radius and height.
Solution : Given that R + H = 6m
\ H = (6 - R)
m
\ Volume of the cylinder
(V)
= pR2H
= pR2
(6 - R)
\ V = 6pR2
- pR3
Differentiating w.r.to R
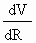 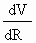
= 12pR
- 3pR2
\ = 0
gives p (12pR
- 3pR2)
= 0
Þ R = 0 or R = 4 Also,  = p
(12 - 6R) = p
(12 - 6R)
Since R ¹ 0, accepting
R = 4, we get
= p (12 - 6 .
4)
= - 12p < 0
\ Volume (V) is maximum when
R = 4
\ The radius of the cylinder
= 4 m and its height = 6 - 4 = 2 m
[next page]
|