|
Example 31
A box is to be made from a sheet 12
´ 12 sq. cm. by cutting equal squares from the four corners
and turning up the sides. Find the length of the side of the square
to be cut of, in order to have a box of the largest possible volume.
Also find the largest volume of the box.

Solution : Let x cm be the length of
the side of the square to be cut off.
Offer cutting of such four squares from four corners
of the sheet 12 ´ 12 sq. cm.
The dimensions of the box to be made are length (L)
= (12 - 2x) cm, breadth (B)
= (12 - 2x) cm and height (H)
= x cm
Now volume of the box (v) = L.B.H
= (12 - 2x) (12 - 2x) x
\ v = 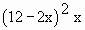
= (144 - 48x + 4x2) x
\
v = 4x3 - 48x2
+ 144x
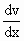 \ \ 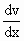 = 12x2
- 96x + 144 = 12x2
- 96x + 144
\ = 12
(x2 - 8x + 12)
\ = 0
Þ (x2
- 8x + 12) = 0
or (x - 6) (x - 2) = 0
OR x = 6 or x = 2 are critical points of which only x = 2 is
acceptable (why ?)
Now  = 24x - 96 = 24x - 96
\ 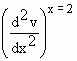 = 24
(2) - 96 = 24
(2) - 96
= - 48 < 0
\ The volume of the box will
be maximum when x = 2.
Therefore the square of side 2cm long must be cut off from each of the corner to get a box of maximum volume. Also L = (12 - 4) 8 cm, and H = 2 cm.
Vmax = 8 ´
8 ´ 2
= 128 sq. cm.
[next page]
|