Example 4

Find the angle between the two curves 2y² = x³ and y² = 32x at their point of intersection in the Ist quadrant

Solution : 2y² = x³ ® (1) and

y² = 32x ® (2)

Solving (1) and (2), we get

2 (32x) = x3

\ x³ - 64x = 0

\ x (x² - 64) = 0

\ x = 0 and x = ± 8

As the point of intersection is in the I^st quadrant it must be +ve and ¹ 0

\ x = 8

Putting in y² = 32x

we get y² = 32(8)

\ y = 256

\ y = ±8

Accepting y = 16, we have the point of intersection is P = (8,16) which lies in the Ist quadrant

Now Differentiating (1) and (2) w. r. to x, we get

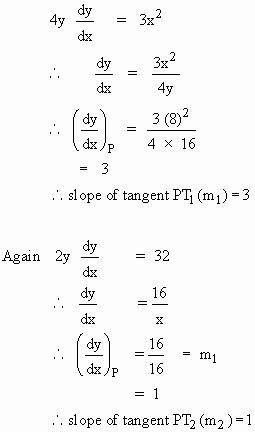
Let q be the acute angle between curves (1) and (2) at P.

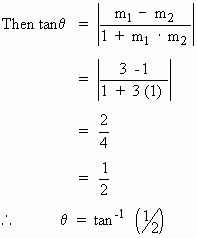
[next page]

Index

5.1 Tangent And Normal Lines
5.2 Angle Between Two Curves
5.3 Interpretation Of The Sign Of The Derivative
5.4 Locality Increasing Or Decreasing Functions 5.5 Critical Points
5.6 Turning Points
5.7 Extreme Value Theorem
5.8 The Mean-value Theorem
5.9 First Derivative Test For Local Extrema
5.10 Second Derivative Test For Local Extrema
5.11 Stationary Points
5.12 Concavity And Points Of Inflection
5.13 Rate Measure (distance, Velocity And Acceleration)
5.14 Related Rates
5.15 Differentials : Errors And Approximation

Chapter 6