|
Example 5
Prove that the curves y2 = 16x and 2x2
+ y2 = 4 cut each other orthogonally.
Solution : Let P (x1, y1)
be a point of intersection of the curves
y2 = 16x ... (1) and
2x2 + y2 = 4 ... (2)
\  = 16x1 ... (3) and
= 16x1 ... (3) and

Let m1 and m2 be the two slopes of the two tangents to the curve (1) and (2) at P respectively.
By Differentiating w. r. to x , the equation (1), we get
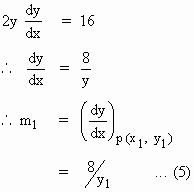
By Differentiating w. r. to x , the equation (2), we get
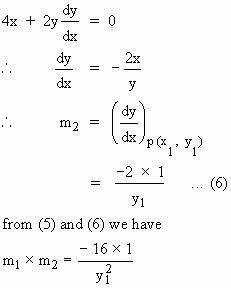
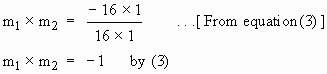
Thus the curves intersect orthogonally at P
[next page]
|