|
Example 4
Draw a graph of y = | x | or y = Öx2
Solution :

The value of y is always the positive for negative and positive values of x. If we replace x by -x the equation remains the same. Therefore, it is symmetrical about y-axis and it lies above x-axis. Also, y increases proportionately as x-increases and as x decreases y too decreases proportionately. Therefore, the graph will have two straight lines in the Ist and IInd Quad.
Example 5
Find the graph of the set { (x,y) | 1£ x £ 3, 0 £ y £ 4 }

Solution :
The graph is the rectangular region of the plane shaded in the figure.
Example 6
Draw the graph of  i.e. arc sin
i.e. arc sin 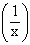

Solution :
Here y is not defined for x = 0. Thus the domain of x is the aggregate of all real numbers except 0. The graph is shown here which is continuous everywhere excepting at x = 0, where a point is missing on the graph. Near O, has an infinite number of oscillations with gradually diminishing amplitude. The graph is comprised between the two lines y = x and y = -x.
|