|
INTRODUCTION
For the study of Calculus, some of the important topics from Algebra, Geometry, Trigonometry and Analytical Geometry are essential. They are briefly summarized below.
Interval Sets:
 Click here to enlarge
Click here to enlarge
Inequalities
It has been aptly remarked that the fundamental results of mathematics are often inequalities rather than equalities. Inequalities are basically related to positivity.
If a, b are positive, so are the product of ab and the sum of a + b.
If a is a number, then either a is positive or a is negative or a = 0, and these possibilities are mutually exclusive.
If a number is not positive and not 0, then it is negative. So if a is negative then - a is positive.
If a is positive and not zero, we write a > 0
If a is positive or zero, we write a ≥ 0
If a - b > 0 it implies that a > b
We write a < 0 if - a > 0 and a < b if b > a
We write a ≥ b if we want to say that a is greater than or equal to b
Thus 6 ≥ 4 and 6 ≥ 6 both are true inequalities.
We give below, in brief, some simple rules concerning inequalities.
1. If a > b and b > c then a > c
2. If a > 0 and b > 0 then ab > 0
3. If a > b and c > 0 then ac > bc
4. If a > b and c < 0 then ab < bc
5. If a < b and a, b, c Î R then a + c < b + c
6. If a > b and c > d then a + c > b + d but a - c  b - d b - d
7. If a > b then - a < - b
8. If a > b > 0 and c > d > 0 then ac > bd
9. If c > b > a > 0 then b - a > 0 and c - a > c - b
10. If b > a > 0 then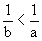
11. If x , y Î R then xy £ 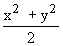
Absolute Value Or Modulus Of A Real Number
Notation:
The absolute value of any number a is denoted by | a|.
Definition 1
The absolute value |a| of a ÎR is defined to be a if a is positive or zero, and to be -a if a is negative.
i.e. | a | = 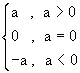
Then | 2 | = 2. Here a = 2 which is greater than 0
| 0 | = 0. Here a = 0
and |- 2 | = - (- 2) ; Here a = - 2 which is less than 0
Definition 2
The absolute value |a | of a Î R is 0 if a Î R = 0. Otherwise |a | is the positive number of the set {a, -a}. Thus, if a = 4 then |a | is the positive of {4, - 4} i.e. 4 ; if a = -3 then |a | is the positive of the set {- 3, - (-3)} i.e. 3
For algebraic manipulations we give still a suitable definition.
[Next page]
|