|
Applications
(A) Roots of a complex number
If p and q are integers relatively prime to each other,
then (cos q + i sin q
)p/q has exactly 'n' distinct roots (i.e. values) which
can be arranged in Geometric progression.
Since cos q and sin q
are periodic functions
\ cos q
= cos (2pk + q)
and sin q = sin (2pk
+ q)
where k is an integer.
Hence (cos q + i sin f
)p/q= [ cos (2pk + q)
+ i sin (2pk + q)
]p/q
= Cos p 
+ i sin p
where k = 0, 1, 2, 3, ...... (q - 1)
These are 'q' different values (roots) of
(cos q + i sin q
)p/q
\ The q values of (cos q
+ i sin q )p/q are
a0, a0b,
a0b2,
a0b3
........, a0bq
- 1
which are obviously in G.P.
Working rule
1) Express (a + ib) in the polar form i.e. a + ib = r (cos q
+ i sin q)
2) Add 2p k to the angle q.
3) Apply De'Moivre's theorem.
4) The required q roots are obtained.
From (3) by putting k = 0, 1, 2, .......(q - 1)
Example 1 Simplify : 
Solution
cos 3q + i sin 3q
= (cos q + i sin q)3........
by De' Moivre's Theorem.
cos 4q - i sin 4q
= (cos q + i sin q)-4
(cos 4q + i sin 4q)
= (cos q + i sin q)4and
(cos 5q + i sin 5q)
= (cos q + i sin q)5
\ The given expression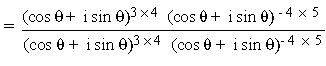 
= (cos q + i sin q)12
- 20 - 12 + 20
= (cos q + i sin q)0
= 1
Example 2
(i) If 2 cos q = 
. Show that 
= 2 cos r q (ii) 
q
Solution
(i) 
= 2 cos q
\ x2
+ 1 = 2 cos q x
i.e. x2 - 2 cos qx + 1 = 0
\ 
\ 
= cos q ± i sin q
\ xr=(cos q
± i sin q)r = cosrq
± i sinrq
Also, 
= cos rq ± i sin rq
Example 3 Express 
in the form a + i b
Solution
Let a + ib = 
b = 1 (1st Quad.)
\ r = 
= 2
and q = tan-1 (b / a) = tan-1 (
) = 300 or 
\ 
= r (cos 300 + i sin 300 )
\ ()7=
[ 2 (cos 300 + i sin 300)]7
=
27[cos 7 ´ 300+
i sin 7 ´ 300]
=
27[cos 2100 + i sin 2100]
=
27 [cos (180 + 30) + i sin (180 + 30
]
=
128 [ - cos 300- i sin 300]
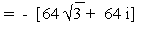
[next page]
|
