|
SUPPLEMENTARY PROBLEMS
(1) Simplify the following
(i) (5 - 9i) ( 7/2 - 5/2i) (ii) 4 - Ö
- 9 ) ( - 2 + Ö 27 )
(iii) (2 + 5i)3

Ans :- (i) 1/2 - 9/2i (ii) ( - 8 + 9 Ö
3 ) + (6 + 2 Ö 3 ) i (iii) - 142
- 65i (iv) (24 / 13) i (v) 1 / 2 .
(2) Express the following in the form a + i b, a, b Î R and
i = Ö-1 
(3) (a) If  show that
show that 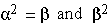
(b) Show that  is a cube root of unity.
is a cube root of unity.
 

(vii) Solve 3x2 + 2x + 1 = 0
Ans :- 
(viii) Solve 2x2 + 3ix + 2 = 0
Ans :- x = -2i, (1/2) i
(ix) Solve ( 3 c is 410) (2 c is197) = 6 c is 2380
where c is q = cosq
+ sin (Sketch it graphically).
(x) Sketch 
(xi) Compute  directly. Change into trigonometric form. and then recompute .
directly. Change into trigonometric form. and then recompute .
(xii) Find all solutions to x6 = Ö
3 - i
Ans :- 1.11819 - 0.0078290i, 0.643818 + 0.96946i, -0.474373 +
1.01730 i,
1.11819 + 0.0978290i, -0.643818 -0.919467i and 0.474373 - 1.01730i
5. Express in the Polar form :-
(i) 3 + 3i
Ans :- 3 Ö 3 (cos 450
+ sin 450 )
(ii) - 4 - 3i
Ans :- 5 (cos 2160 52' + i sin 2160 52')
(iii) - 12 + 5i = 13 (cos 1570 23' + i sin 1570
23')
(iv) - 2i = 2 (cos 2700 + i sin 2700)
6. Use DeMoivre's Theorem to evaluate :-
(i) ( Ö 3 / 2 i / 2 ) 9
Ans : - i
(ii) (1 + i)8 Ans :- 16
(iii) (3 + 4i)4 Ans : - 526.9 - 336. 1 i
(iv) (1/ 2 - i Ö 3 / 2)
20 Ans :- - 1/2 - i Ö 3
/ 2
 Ans :- 1 - i
Ans :- 1 - i

**********
[next page]
|