|
4.4 Tangent Identities
1) Sum and Difference Identities
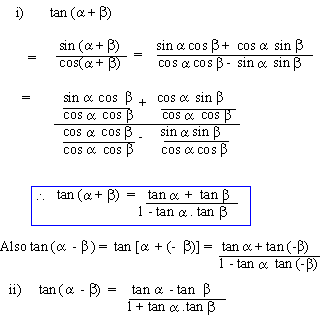
Double (Multiple) angle and Half (sub
multiple) angle Identities
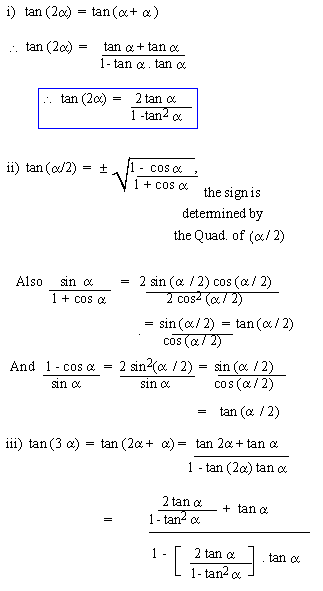
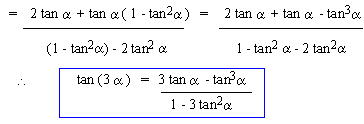
EXAMPLE 1 Prove that tan 200
+ tan 250+ tan 200 (tan 250) =
1
Solution :
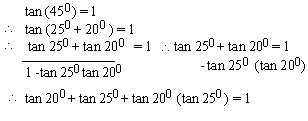
EXAMPLE 2 Find tan 750
Solution:
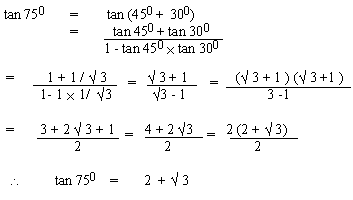
EXAMPLE 3 Prove that tan 500=
tan 400 + 2 tan 100
Solution:
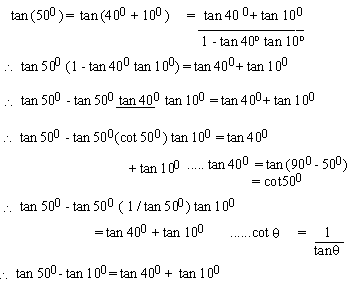
\ tan 500
- tan 400 + 2 tan 100
EXAMPLE 4 If A + B = p
/4, then prove that ( 1 + tan A ) (1 + tan B) = 2
Solution :
\ A + B = p/4
ie, 450
\ tan (A + B ) =
tan ( 45 0 )
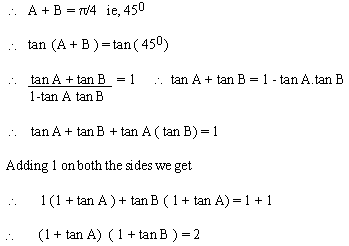
EXAMPLE 5 Evaluate 
Solution :
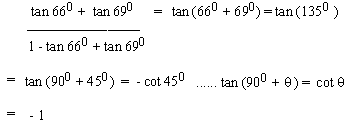
EXAMPLE 6 If tan x = 5 / 6
and tan y = 1 / 11. Show that x + y = p
/ 4 rad.
Solution:
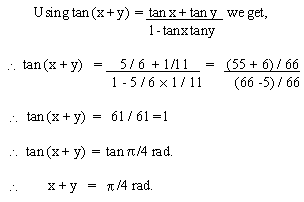
EXAMPLE 7 Find the value of
tan (a + b)
where a is in Quad III and b is in Quad .II such that cos a
= -3/5 and sin b = 20/29.
Solution: Since cos a
= -3/5
\ sin2a
= 1 - cos2a
\ sin2 a=
1 -9/25 =16/25
\ sin a
= -4/5, sine is negative in Quad III.
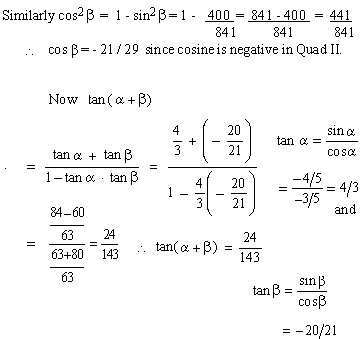
EXAMPLE 8 Using half -angle
identity find tan 150
Solution:
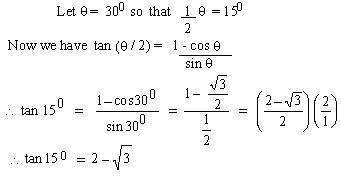
[next page]
|