4.1 Fundamental Identities

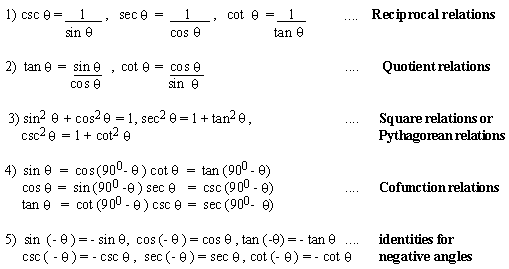
Click here to enlarge

Unfortunately no standard (or general) method of proof of identities exists which works for all identities. However, here is a list of some hints or general rules or strategies that we can suggest.

1. Work with more complicated side (if there is one) till it matches the second side.

2. If you are unable to reduce one side to the other, use the fundamental identities (1) and (2) to change eveything into sines and cosines.

3. Apply the Pythagorean identities i.e. sin2 + cos2 = 1 or the other forms
   cos ² = 1 - sin² = ( 1 + sin ) (1 - sin ),
   sin² = 1 - cos ² = ( 1 + cos ) (1 - cos ),
   sec² - tan² = 1 or (sec + tan ) (sec - tan ) =1 etc.

4. Above all, at evey step keep your eye on the expression that you want to end with this only dictates your ways of proving the identities.

SOLVED EXAMPLES : (Type - I)

Example 1 If find csc , tan , cot and

Solution

We know that 3p/2 < < 2 p i.e, 270⁰ < ⁰ < 360⁰ i.e. lies in the IV th Quadrant. Using `ASTC' sin , csc , tan and cot are negatives. only cos and sec are positive.

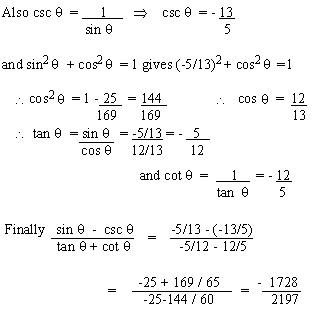
Example 2 If sin = 7 / 8, cos < 0 . Determine other 5 values of the trigonometric ratios.

Solution: sin² + cos ² = 1

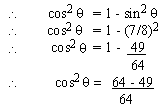
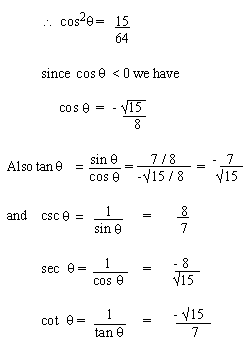
[next page]

Index

Trignometric Identities

4.1 Fundamental Identities
4.2 The addition formulas
4.3 The multiple-angle (Double & Half angle) formulas
4.4 Tangent Identities
4.5 Factorization & Defactorization

Supplementary Problems