|
TYPE III
Example 1 Prove that 
Solution
 ...Identity
to be verified.
Example 2 Verify that cos
a + sin a
tan a = sec a
Solution
cos a + sin a
tan a = sec a
...identify to be verified.
Example 3 Prove that cot 
+ tan = cosec
sec
Solution
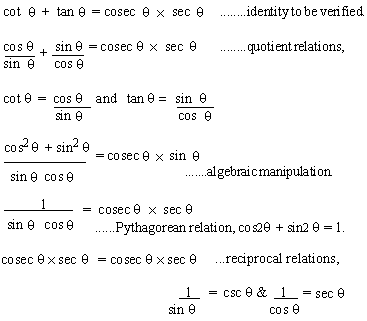
Example 4 sin4
A - cos4 A = 1- 2 cos2A Prove this!
Solution
sin 4 A - cos4A = 1 - 2cos2
A ....identity to be verified.
(sin2 A - cos 2A) (sin
2 A + cos2A) = 1 - 2cos2 A ...factorizing.
(sin2 A - cos2A) 1 = 1 -
2 cos 2A ....Pythagorean relation.
1- cos2 A - cos 2A = 1-
2 cos 2A .....Pythagorean relation, sin2A=
1- cos2 A
\ 1 - 2 cos2
A = 1 -2 cos2A .... algebric manipulation.
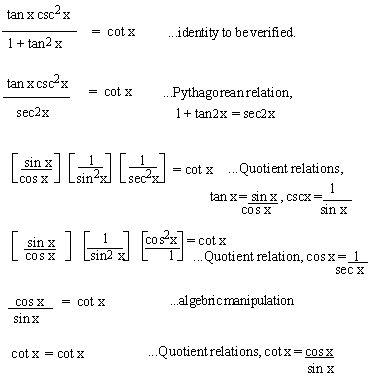
Example 5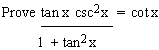 
Solution
Example 6 Prove tan2
- sin2 =
tan2 
sin2
Solution
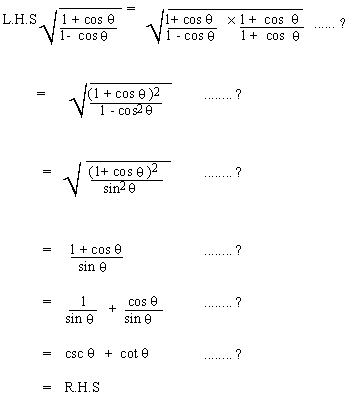
Example 7 
= csc + cot
Prove.
Solution
Note : reasoning is left to
you.
Example 10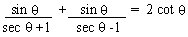
Solution
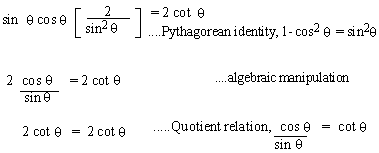
Example 9
Verify that 
Solution
Example 10 
Solution
\ tan A. tan B = tan
A tan B
Example 11
 Prove
this !
Solution
To prove this identity, it is advisable to rearrange
the terms, then the example is, to prove that,
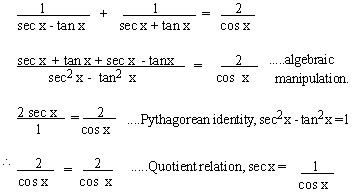
[next page]
|
