|
Example 2 A particle is moving along x-axis. Its distance x from the origin at time t is given by
x = 3 cos 2t + 4 sin 2t + 6. If the motion is S.H.M. , find the centre of the motion, period and amplitude.
Solution
Since the motion is S.H.M., its acceleration at any time t is proportional to its displacement from
the point X = 0 i.e. x = 6 since x = 3 cos 2t + 4 sin 2t + 6 Þ x - 6 = 3 cos 2t + 4 sin 2t.
Let x - 6 = X
Thus the particle executes S.H.M. about its centre at x = 6
Now comparing X = 3 cos 2t + 4 sin 2t with
X = A cos wt + B sin
wt
we get
A = 3, B = 4 and w = 2
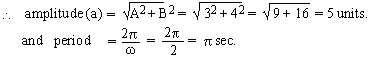
Example 3
At the end of three successive seconds, the distances of a particle executing
a S.H.M. from the center are u, v and w. Show that the periodic time of S.H.M. is 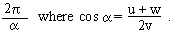
Solution
Since the periodic time is to be T = 2p / a , the constant of S.H.M. is a. Hence the equation
of S.H.M. be x = a sin (wt + b) and let u, v and w be the distances of the particle at the ends of t,
t + 1 and t + 2 seconds respectively. Then
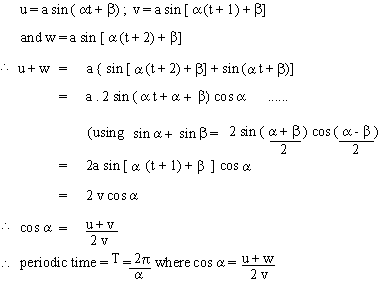
Example 4 A body describes simultaneously two motions,
x1 = 3 sin 40t, x2 = 4 sin 41t
What is the maximum and minimum amplitude of combined motion and what is the beat frequency ?
Solution
If a body is subjected to two harmonic motions given by x1 = a sin w1t and x2 = b sin w2 t
\ Maximum amplitude is (a + b) and minimum amplitude (a - b). Therefore in this problem
the maximum amplitude = 3 + 4 = 7 units and the minimum amplitude = 4 -3 = 1 units.
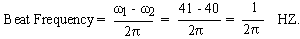
|