Example 2

Evaluate

1)

Solution

j² = -1, j³ = j² ´ j = - j, j⁴= (j²)²= (-1)² = 1 and j⁵ = j⁴ ´ j = (1) j = j
then = 4

Example 3
Perform the indicated operations.

(a) ( 4 - 2i) + (- 6 + 5i) = 4 - 2i - 6 + 5i = (4 - 6) + (-2 + 5) i = -2 + 3i
(b) (-7 - 3i) - (2 - 4i) = (-7 -2) + (-3 + 4) i = -9 + i
(c) (3 - 2i) (1 + 3i) = 3 (1 + 3i) - 2i (1 + 3i) = 3 + 9i - 2i - 6i² = 3 + 9i - 2i + 6 = 9 + 7i
(d)

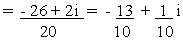
Example 4
Simplify

a)

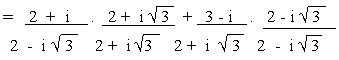
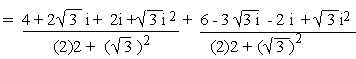
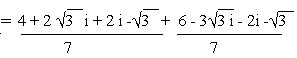
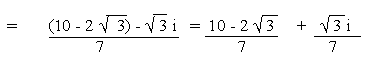
b)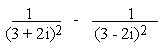

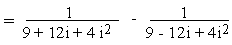
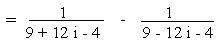
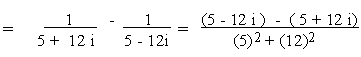
Example 5

Find the real values of 'a' and 'b' if
(a)       (a - 2bi) + (-b - 3ai) = 5 + 2i

Solution

(a - b) + (-2b -3a)i = 5 + 2i. Equating the real and imaginary parts, we get

a - b = 5 ....(1) and - 2b - 3a =2 .......(2) solving we get

a = putting a = in

(1) - b = 5

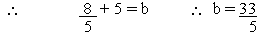
(b)      (2 - 3i) (4i + 5) = a + bi

Solution

[next page]

Index

8.1 Geometry of complex numbers
8.2 De - Moivres's theorem
8.3 Roots of complex numbers
8.4 Cirsular functions of complex angles & hyperbolic function
Supplementary Problems

Chapter 9