|
EXAMPLE 13
Solve : 3 sin x + 4 cos x = 2
Solution : 3 sin x + 4 cos x = 2 \ a = 3, b = 4 and c = 2
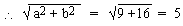
Dividing by 5 to the given equation
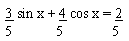
i.e. 0.6 sin x + 0.8 cos x = 0.4
\ sin 360 52' sin x + cos 360 52' cos x = cos 660 25'
i.e. cos (x - 3600 52') = cos 660 25'
The general solution is x - 360 52' = n (3600) ± 66.25'
i.e. x = n (3600) + 1030 17' or n (3600) - 290 33'
EXAMPLE 14
Solve cos 2x = 3 (sin x - 1) for all values of x
Solution : cos 2x = 3(sin x -1)
1 - 2 sin 2x = 3 sin x -3 ..........( since cos 2x = 1 - 2 sin 2x)
2 sin 2x + 3 sin x - 4 = 0
Comparing with ax2 + bx + c = 0 form,
a = 2, b = 3 and c = - 4
Then using 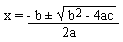
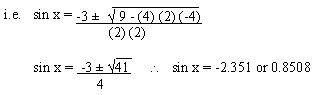
since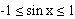 then -2.351 is impossible. then -2.351 is impossible.
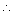 Taking sin x =0.8508 Taking sin x =0.8508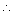 x =1.0175 in radians. x =1.0175 in radians.
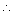 x = 58.30 + 2n x = 58.30 + 2n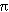 in degrees. in degrees.
x = 58.30 + n(3600)
and x = 2.124 + 2n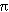 or x = 121.7
0 + n (3600) or x = 121.7
0 + n (3600)
[next page]
|