|
3.2 Law Of Cosines
If A, B and C are the measure of angles of a triangle
ABC and a, b and c are lengths of sides opposite the angles A, B
and C respectively, then

These three formulas are called the Law of cosines
or cosine rule. Let us place angle A of triangle ABC in standard
position. Further Ð A < 1800
therefore point C is above x-axis. In two figures, Ð
A is as acute and obtuse.
... AB = C \
B º (c, 0). Let C º
(x, y). Since AC = b.
We have x = b cos A and y = b sin A
\ C º
( b cos A, b sin A). Now BC = a
By using distance formula
(BC)2 = (c - b cos A)2 + (b sin A)2
\ a2 = c2 -
2bc cos A + b2 cos2 A + b2 sin2
A
\ a2 = c2 -
2bc cos A + b2 (cos2 A + sin2
A)
\ a2 = c2 - 2bc cos A +
b2 (1)
\ a2 = c2 -
2bc cos A + b2
\ a2 = b2 +
c2 - 2bc cos A OR
\ 
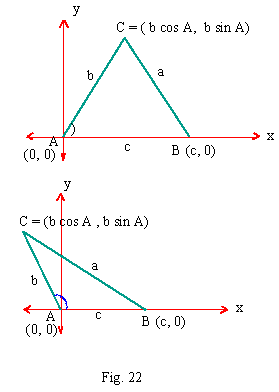
Note that if A = 900 , then cos A =
cos 900 = 0, giving a2 = b2 + c2
which is the "Pythagoras theorem" for right triangles.
If the orientation of the triangle is changed to have B or C at
the origin, then the other two versions of Law of cosines can be
obtained.
[next page]
|