|
Example 9
The angle of elevation of the top of a pole is
150 from a point on the ground. On walking 100 feet towards
the pole the angle of elevation is found to be 300 .
Find the height of the pole.
Solution
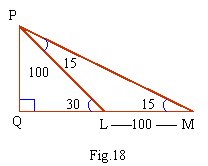
Let PQ be the pole from point M when observed at
P, ÐPMQ = 150. In the
direction MQ when walked 100 feet to point L, Ð
PLQ = 300 . Now ÐPLQ
is the exterior angle of triangle PML \
Ð PML + Ð
MPL = 300 . But Ð PML
= 150
\ Ð
MPL = 150
i.e. Triangle is an isosceles triangle
ML = PL = 100 feet
Now from triangle PLQ, sin 300 = 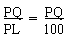
\ PQ = 100 ´
sin 300= 100 ´
1/ 2 = 50
Hence PQ = 50 feet
\ Height of the pole is 50 feet.
Example 10
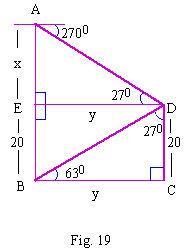
When seen from the top and bottom of a tower towards
the top of a building, the angle of depression and the angle of
elevation are 27 0 and 630 respectively. If
the height of the building is 20 m. Find the height of the tower.
Solution
DC = 20 m, DE = 20 m. Let AE = x, BC = y
Now in right triangle BCD, tan 270 = 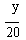

[next page]
|