Example 3

The width of a road is 13 m. Two buildings are at both end of the road opposite to each other. One is 35m high. If from the top of this building the top of the another building is viewed, the angle of elevation is 37⁰. Whate is the height of the other building ?

Solution : From the fig. Ž ABCD is a rectangle.

\ AB = CD = 35 m

\ BC = AD = 13 m

Let ED = x meters

Now in right triangle EAD, tan 37 =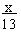

\ 0.7585 = 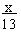\ x = (0.7535) (13) = 9.802 m

Again CE = CD + ED = 35 + 9.802 = 44.802 m

\ Height of the another building is 44.802 m.

Example 4

A ladder on a firetruck can be extended to maximum length of 20 m, when elevated to its maximum angle 70⁰. The base of the ladder is mounted on the truck 2m above the ground. How high above the ground will the ladder reach ?

Solution : From the fig. Ž BDEC is a rectangle

\ BD = CE = 2 m. Let AB = x

Now sin 70⁰ = \ 0.94 = \ x = (0.94) (20)

\ x = 18.8 . Again AD = AB + BD

       = 18.8 + 2 = 20.8 m

\ The ladder can reach the height of 20.8m above the ground.

[next page]

 

Index

3. 1 Solving Right Triangles
3. 2 Law of Cosines
3. 3 Law of Sines
3. 4 The Ambiguous Case of Law of Sines
3. 5 Areas of Triangles
Supplementary Problems

Chapter 4