| SUPPLEMENTARY PROBLEMS
(1) Find the natural t-ratios of each of the following
angles (1) 180 47' (2) 580 24' (3) 79
0 45'.
Answer :
Click here to enlarge
(2) Find the values of the trigonometric functions
of q, given :
(a) cos q = - 4 / 5 (b) sin q
= - 2 / 3 (c) tan q = 3 / 5 (d) sec q
= 
Answer : (a) Quad II : 3 / 5, - 4 / 5, - 3 / 4, - 4 / 3, - 5 / 4,
5 / 3
Quad III : - 3 / 5, - 4 / 5, 3 / 4, 4 / 3, - 5 / 4, - 5 / 3
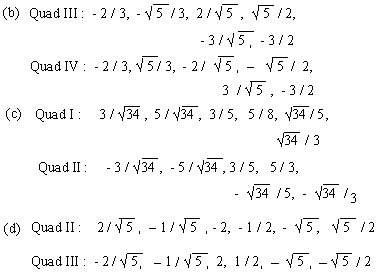
(3) Find the five coterminal angles for an angle
of measure - 700 .
Answer : 2900 , 6500, 10100, -
4300, - 7900
(4) Find the values of t-ratios of the acute angles
of the right triangle ABC, given that
(a) a = 2, c = 5 (b) b = 
, c = 4
Answer :
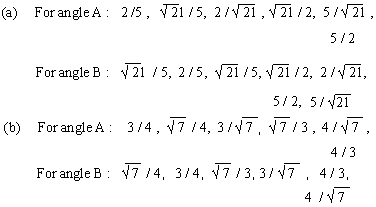
(5) Using the definitions, find the values of
(i)  (iv)
sec 3300
Answer :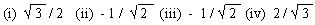 
(6) Verify the following using the tables
- cos 300 cos 600 + sin 300
sin 600 =
- 4 cos3450 - 3 cos 450 = -
sin 450
- 4 cot2 (p / 6) - 5 sec2
(p / 4) + 6 csc2 (p
/ 3) - 7 cos2 (p / 2) =
10
- cos2300 + sin2 600
+ sin2 900 + cos21800
= 7 (sin2450 + cos2 900
)
v.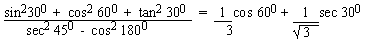 
(7) Find the acute angles A and B satisfying
(i) tan (A + B) =  and
cosec (A - B) = 2
Answer : - A = 450 or B = 150
(ii) 2 cos A tan B - 2 cos A - tan B + 1 = 0
Answer :- A = 600 or B = 450
(iii) 2 cos2 q - 2 
cos q + 1 = 0
Answer :- q = 300 or 60
0
(iv) 3 tan2 q - 4
tan q + 3 = 0
Answer : - q = 300 or 600
(8) (i) Solve the right triangle ABC, given that
Ð B = 900 , a = 40 cms,
b = 65 cms.
Answer :- Ð A = 370
59' , Ð C = 520 1' c
= 51.23 cms.
(ii) Solve the triangle ABC, given that Ð;
A = 900 , AB = 36m and BC = 64 m
Answer :- Ð; C = 340 10'
, Ð B = 550 50' , b =
52.95 m
(iii) Solve the triangle ABC, given that Ð
A = 66 0 36' , a = 112.6 .
Answer :- Ð B = 230
24' , b = 48.73 , C = 122.7.
(9) The base of an isosceles triangle is 15.90
cms and the base angles are 540 28' . Find the equal
sides and altitudes.
Answer :- 13.68 cms, altitude = 11.13 cms.
(10) A wall 15 m high and 10 m from a house. Find
the length of the shortest ladder which will just touch the top
of the wall and reach a window 20.5 m above the ground.
Answer : - 42.5 m.
**********
|
