|
2.3 Functions of General Angles or t -Ratios
Draw a unit circle (circle of radius 1 unit).
Let O be the centre of this unit circle. Set a rectangular right-hand
co-ordinate system, taking O as its origin (see fig).
Let the circle cut the x-axis at A º
(1,0). Rotate OA around O (counter clockwise or clock wise) reaching
OP and forming an angle of measure q
.
Obviously OP = 1 unit.
Let P º (x, y)
then we define the following
1. sin q = y / r or
y / 1 = y (\ r = 1)
2. cos q = x / r or
x / 1 = x (\ r = 1)
3. tan q = y / x provided
x ¹ 0
4. cot q = x /y provided
y ¹ 0
5. csc q = r /y = 1/y
provided
y ¹ 0
6. sec q = r/x = 1/x
provided x ¹ 0
Note : Whenever we wish to
find the values of t- ratios of standard angles or prove some result,
we shall say "Draw a unit standard circle and let angle q
be in standard position." This will automatically mean that
the initial side of the angle is along the x-axis, vertex being
at the origin.
The Signs Of Trigonometric Ratios
Since r is always positive, the signs of the functions
in various quadrant depend upon the signs of x and y. To determine
these signs one may visualize the angle in standard position.
1) If P(x, y) be in the 1st quadrant both x and
y are positive. Hence all t-ratios are positive.
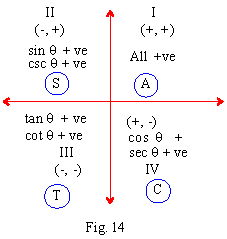
2) If P (x, y) be in the IInd quadrant x is negative
and y is positive.
\ sin q
= y / r , csc q = r / y are positive
cos q = x / r, sec
q = r / x, tan q
= y / x and cot q = x / y are all negative
3) If P (x,y) be in the IIIrd quadrant, both x
and y are negative.
Hence sin q y /r , cos q
= x / r, csc q = r / y
and sec q r / x are all negative whereas
tan q = y / x and cot q
= x / y are positive.
4) If P(x, y) be in the IVth quadrant, x is positive
but y is negative.
Hence cos q = x / r
and sec q = r /x are positive but sin
q = y / r, csc q
= r / y, tan q = y /x and cot
q = x/y are all negative.
A crude aid to remember the signs is the four letter
acronym (phrase) ASTC which stands for All Silver Tea Cups or "Arizona State Teacher's College" or any other four worded
phrase that will help you to remember the relationships.
Note:
| A |
S |
T |
C |
| ¯ |
¯ |
¯ |
¯ |
|
All are +ve In Ist quad.
|
sine and csc. are +ve in II quad. |
tan and cot are +ve in III quad |
cos and sec are + ve in IV quad |
Trigonometric Ratios Of Quadrantal Angles
For these angles the terminal side of an angle
coincides with one of the co-ordinate axes. Therefore point P(x,
y) on the terminal side has either x = 0, y ¹
0 or x ¹ 0, y = 0. In either case,
two of the six t-ratios are not defined. For instance, for angle
00 terminal side coincides with +ve of x-axis and its ordinate i.e
y = 0. Now cot q = x / y and csc q
= r / y, having y = 0 in the denominator are not defined. Some authors
write this as cot 00 = ±
¥ or simply cot 00 = ¥
.
The t- ratios of the quadrantal angles are :-
Click here to enlarge
|
