|
(4) Find the area of the shaded portion of the sector of the circle
shown in the given figure.
Solution
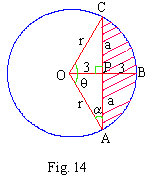OA = OB = OC = 6 ........ (Radii of the same circle)
\ r = 6
In rt. angled D OPA, by Pythagoras theorem,
r2 = 32
+ a2
\ 62 - 32= a2
\ 27 = a2
\ a = 3 Ö
3
Also sin a =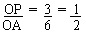 
\ a = sin-1
(0.5) = 300 \ a
= p/6 rad
Since in rt. angled D OPA,
a = 30 0 , Ð P
= 90 0
we have Ð POA = 60 0
then it follows that q = 120 0
=  
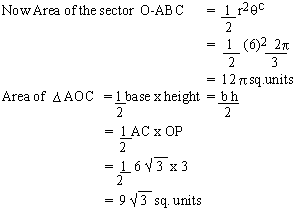
Area of the shaded portion = Area of the sector O-ABC -Area of
D AOC
= 12 p - 9 Ö
3 = 3 (4p - 3Ö
3 )
» 22.11 sq. units.
(5) In a circle of radius 6 cm. an arc PQ subtends an angle of
300 at the centre. Find the area between arc PQ and chord
PQ.
Solution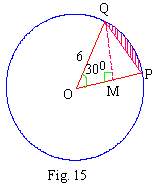 
Let O be the centre of the circle.
\ OP = OQ = 6 cms ........ (Radii)
\ r = 6 cms.
Also m ÐPOQ = 300 =
p/6 rad
\ q = p/6
rad
Area of sector O-PQ =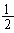 
OP2 ´
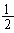q = (6)2
´ 
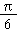
= 3 p sq. units
|
