|
To find the area of the D OPQ. Draw QM ^
OP.
Since Ð POQ = 300 we
have QM = 1/2 (OQ) = 3 cms.
Area of the D OPQ = 1/2 OP. QM = 1/2
x 6 x 3 = 9 sq. cm.
Area of the shaded portion = area of sector - area of triangle
= (3p - 9) sq. cm
= 3 (p - 3) sq. cm
» 3(3.14 - 3) sq. cm
» 0.42 sq. cm
(6) Two circles each of radius 5 cms intersect
each other. If the distance between their centre is 5 Ö2
cms. Find the area common to the circles.
Solution 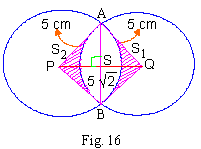
From the fig. It is clear that PQ2 = PA2 +
QA2
Since (5 Ö2 )2 = (5)2
+ (5)2 i.e 50 = 25 + 25
\ By the converse of Pythagoras theorem,
D PAQ is a right D
with Ð A = 900 and
Ð APQ = 450
\ Ð
APB = 900 Let APB = q = 900
= p/2 rad
Now area of sector P - AB = 1/2 r 2 qc
= 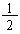 (5)2
p/2 (5)2
p/2
= 25/4 p sq.cms
Also Area of square APBQ = (side) 2 = (5) 2
= 25 sq. cms. 
|