|
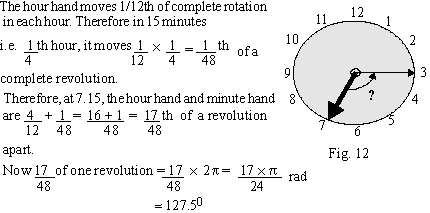
(2) What is the angle measure, in radians of the
acute angle formed by the minute hands of a clock at 7.15 with hour
hand ?
Solution
(3) Two concentric circles with centre at O and
radii 5cms and 10 cms are drawn. A straight line OP drawn through
the centre cuts them in A and A' respectively. This line is rotated
through 600 and in its final position it cuts the circles in B and
B' respectively. Find the perimeter and the area of the portion
between the two circles and the two lines.
Solution
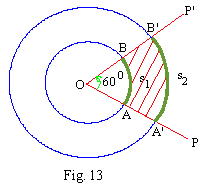
(i) We have OA = 5 cms, OA' = 10 cms, q
= 600 = p/3 rad.
\ AA' = 5 cms Similarly BB' = 5 cms
Also q = 600 = p/3
rad
Let arc AB = s1 and arc A'B' = s2
then considering the inner circle and using s = r qc
we get
s1 = 5 ´ p
/ 3 = 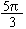 cms cms
Similarly for arc A'B' = s2 = 10 ´ 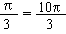 cms cms
\ the perimeter of the required portion
(shaded portion)
= AB + BB' + A'B' + AA'
= s1 + BB' + s2 + AA'
= 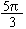 + 5
+ + 5
+ 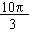 + 5 + 5
= 10 + 5p = 5 (p
+ 2) » 5 (3.14 + 2) »
5 (5.14)
= 25.70 cms.
(ii) Area of the portion ABB'A'A (shaded)
= Area of sector O - A'B' - Area of sector O - AB
= 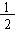 OA'2qc
- OA'2qc
- 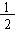 OA2qc ......
(by using A = 1/2 r2 qc
)
OA2qc ......
(by using A = 1/2 r2 qc
)
= 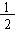 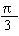 (102 - 52 ) sq. cms.
(102 - 52 ) sq. cms.
= 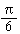 (100
- 25) sq. cms (100
- 25) sq. cms
= 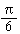 75
sq. cms 75
sq. cms
= 12.5 p sq. cms
= (12.5) (3.14) sq. cms
A (ABB'A'A) = 39.25 sq. cms (approx)
|